Peterson’s Algorithm: Complete Guide to Two-Process Mutual Exclusion in Operating Systems

What is Peterson’s Algorithm?

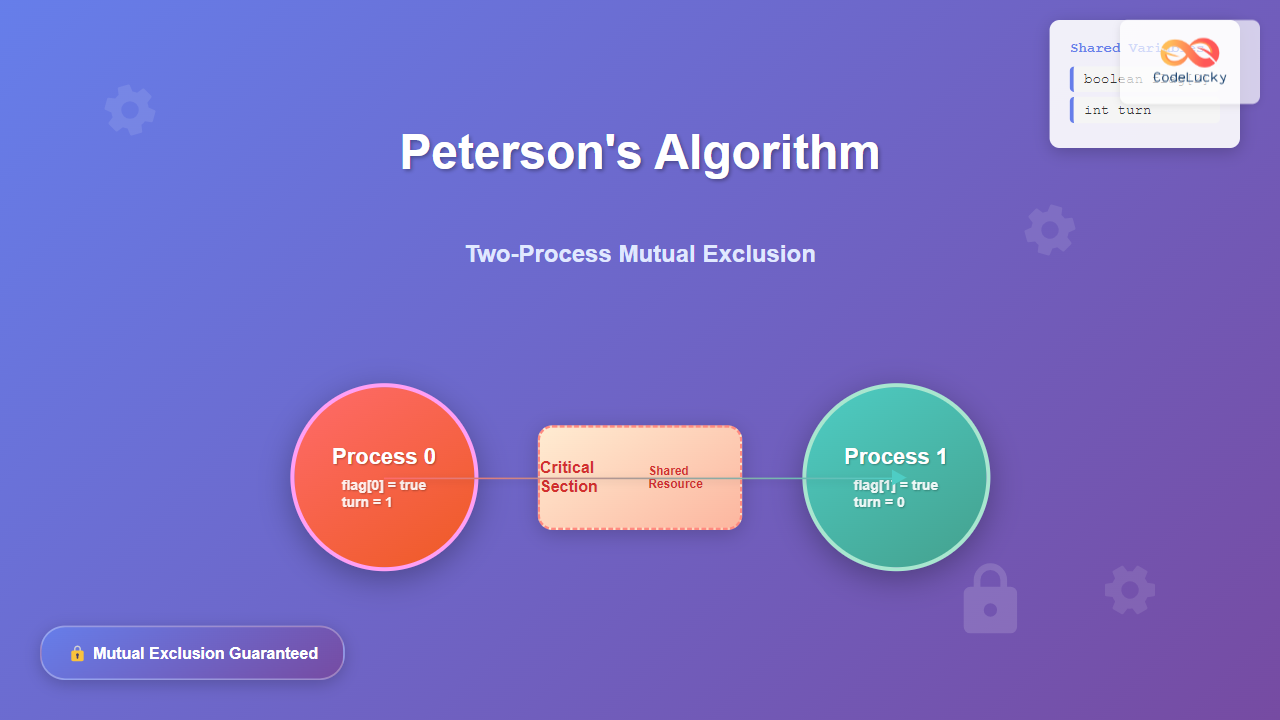
Peterson’s Algorithm is a classic solution for achieving mutual exclusion between two processes or threads in concurrent programming. Developed by Gary Peterson in 1981, this algorithm ensures that only one process can access a critical section at a time, preventing race conditions and data inconsistency.

Unlike hardware-based solutions, Peterson’s Algorithm relies purely on software mechanisms using shared variables and careful coordination between processes. It’s particularly valuable for understanding the fundamental principles of process synchronization in operating systems.

The Mutual Exclusion Problem

Before diving into Peterson’s Algorithm, let’s understand the core problem it solves:

• Critical Section: A code segment where shared resources are accessed
• Race Condition: When multiple processes access shared data simultaneously, leading to unpredictable results
• Mutual Exclusion: Ensuring only one process executes in the critical section at any given time

How Peterson’s Algorithm Works

Peterson’s Algorithm uses two shared variables to coordinate between processes:

1. flag[2]: Boolean array indicating each process’s intention to enter the critical section
2. turn: Integer variable indicating whose turn it is to enter the critical section

Algorithm Structure

Each process follows this pattern:

// Shared variables
boolean flag[2] = {false, false};
int turn = 0;

// Process i (where i = 0 or 1)
void process_i() {
    while (true) {
        // Entry section
        flag[i] = true;           // Show intention to enter
        turn = 1 - i;             // Give turn to other process
        while (flag[1-i] && turn == 1-i) {
            // Busy wait
        }
        
        // Critical section
        // ... critical code here ...
        
        // Exit section
        flag[i] = false;          // No longer interested
        
        // Remainder section
        // ... non-critical code ...
    }
}

Detailed Step-by-Step Execution

Let’s trace through the algorithm execution with two processes P0 and P1:

Case Analysis

Case 1: Both processes want to enter simultaneously

// Initial state: flag[0] = false, flag[1] = false, turn = 0

// Process 0 executes:
flag[0] = true;    // P0 shows intention
turn = 1;          // P0 gives turn to P1

// Process 1 executes:
flag[1] = true;    // P1 shows intention  
turn = 0;          // P1 gives turn to P0

// Now turn = 0 (last assignment wins)
// P0 checks: flag[1] && turn == 1 → true && false → false (enters CS)
// P1 checks: flag[0] && turn == 0 → true && true → true (waits)

Properties of Peterson’s Algorithm

Peterson’s Algorithm satisfies all three requirements for a correct mutual exclusion solution:

1. Mutual Exclusion

Only one process can be in the critical section at any time. This is guaranteed because:

• If both processes try to enter, the turn variable ensures only one succeeds
• The condition flag[1-i] && turn == 1-i prevents simultaneous entry

2. Progress

If no process is in the critical section and some processes want to enter, one of them will eventually enter. The algorithm doesn’t create deadlocks.

3. Bounded Waiting

A process waiting to enter the critical section will eventually get its chance. No process can be indefinitely postponed.

Complete Implementation Example

Here’s a complete C implementation demonstrating Peterson’s Algorithm:

#include <stdio.h>
#include <pthread.h>
#include <unistd.h>

// Shared variables
volatile int flag[2] = {0, 0};
volatile int turn = 0;
volatile int shared_counter = 0;

void* process0(void* arg) {
    for (int i = 0; i < 5; i++) {
        // Entry section
        flag[0] = 1;
        turn = 1;
        while (flag[1] && turn == 1) {
            // Busy wait
        }
        
        // Critical section
        printf("Process 0 entering critical section\n");
        int temp = shared_counter;
        usleep(1000); // Simulate some work
        shared_counter = temp + 1;
        printf("Process 0: shared_counter = %d\n", shared_counter);
        
        // Exit section
        flag[0] = 0;
        
        // Remainder section
        usleep(1000);
    }
    return NULL;
}

void* process1(void* arg) {
    for (int i = 0; i < 5; i++) {
        // Entry section
        flag[1] = 1;
        turn = 0;
        while (flag[0] && turn == 0) {
            // Busy wait
        }
        
        // Critical section
        printf("Process 1 entering critical section\n");
        int temp = shared_counter;
        usleep(1000); // Simulate some work
        shared_counter = temp + 1;
        printf("Process 1: shared_counter = %d\n", shared_counter);
        
        // Exit section
        flag[1] = 0;
        
        // Remainder section
        usleep(1000);
    }
    return NULL;
}

int main() {
    pthread_t t0, t1;
    
    pthread_create(&t0, NULL, process0, NULL);
    pthread_create(&t1, NULL, process1, NULL);
    
    pthread_join(t0, NULL);
    pthread_join(t1, NULL);
    
    printf("Final shared_counter value: %d\n", shared_counter);
    return 0;
}

Expected Output

Process 0 entering critical section
Process 0: shared_counter = 1
Process 1 entering critical section
Process 1: shared_counter = 2
Process 0 entering critical section
Process 0: shared_counter = 3
Process 1 entering critical section
Process 1: shared_counter = 4
...
Final shared_counter value: 10

Advantages and Limitations

Advantages

• Pure software solution: No special hardware instructions required
• Provably correct: Mathematically proven to satisfy all mutual exclusion requirements
• Simple implementation: Uses only basic programming constructs
• Educational value: Excellent for understanding synchronization principles

Limitations

• Busy waiting: Wastes CPU cycles while waiting
• Two processes only: Cannot be extended to more than two processes
• Memory consistency: Requires strong memory ordering guarantees
• Performance overhead: Continuous polling can be inefficient

Modern Alternatives and Applications

While Peterson’s Algorithm is primarily of historical and educational significance, modern systems typically use:

• Mutex locks: Operating system provided synchronization primitives
• Semaphores: Generalized synchronization mechanism
• Atomic operations: Hardware-supported atomic instructions
• Lock-free algorithms: Advanced techniques avoiding locks entirely

When to Use Peterson’s Algorithm

Peterson’s Algorithm is still relevant in:

• Educational contexts: Teaching mutual exclusion concepts
• Embedded systems: Resource-constrained environments
• Research: Theoretical analysis of synchronization algorithms
• Interview preparation: Common computer science interview topic

Memory Consistency Considerations

On modern processors with relaxed memory models, Peterson’s Algorithm may not work correctly without proper memory barriers. The algorithm assumes that memory operations are executed in program order, which isn’t guaranteed on all architectures.

// Modern implementation with memory barriers
void process_i() {
    while (true) {
        flag[i] = true;
        __sync_synchronize(); // Memory barrier
        turn = 1 - i;
        __sync_synchronize(); // Memory barrier
        
        while (flag[1-i] && turn == 1-i) {
            // Busy wait
        }
        
        // Critical section
        // ... critical code ...
        
        __sync_synchronize(); // Memory barrier
        flag[i] = false;
    }
}

Conclusion

Peterson’s Algorithm represents a milestone in concurrent programming, providing an elegant software-only solution to the two-process mutual exclusion problem. While modern systems have moved beyond this approach for practical applications, understanding Peterson’s Algorithm remains crucial for:

• Grasping fundamental synchronization principles
• Appreciating the evolution of concurrent programming
• Building foundation knowledge for advanced synchronization techniques

The algorithm’s beauty lies in its simplicity and correctness, using just two shared variables to solve a complex coordination problem. For computer science students and professionals, Peterson’s Algorithm serves as an excellent introduction to the challenges and solutions in concurrent programming, paving the way for understanding more sophisticated synchronization mechanisms used in modern operating systems.