Derivatives: Options Greeks for Beginners – Understanding Delta, Gamma, Theta, Vega & Rho

In the world of derivatives, understanding Options Greeks is essential for every trader. Whether you’re analyzing risk, designing a hedging strategy, or fine-tuning your portfolio, the Greeks help you measure how an option’s price moves with respect to variables like price, time, and volatility. This guide simplifies these concepts using visual explanations, examples, and beginner-friendly analogies.

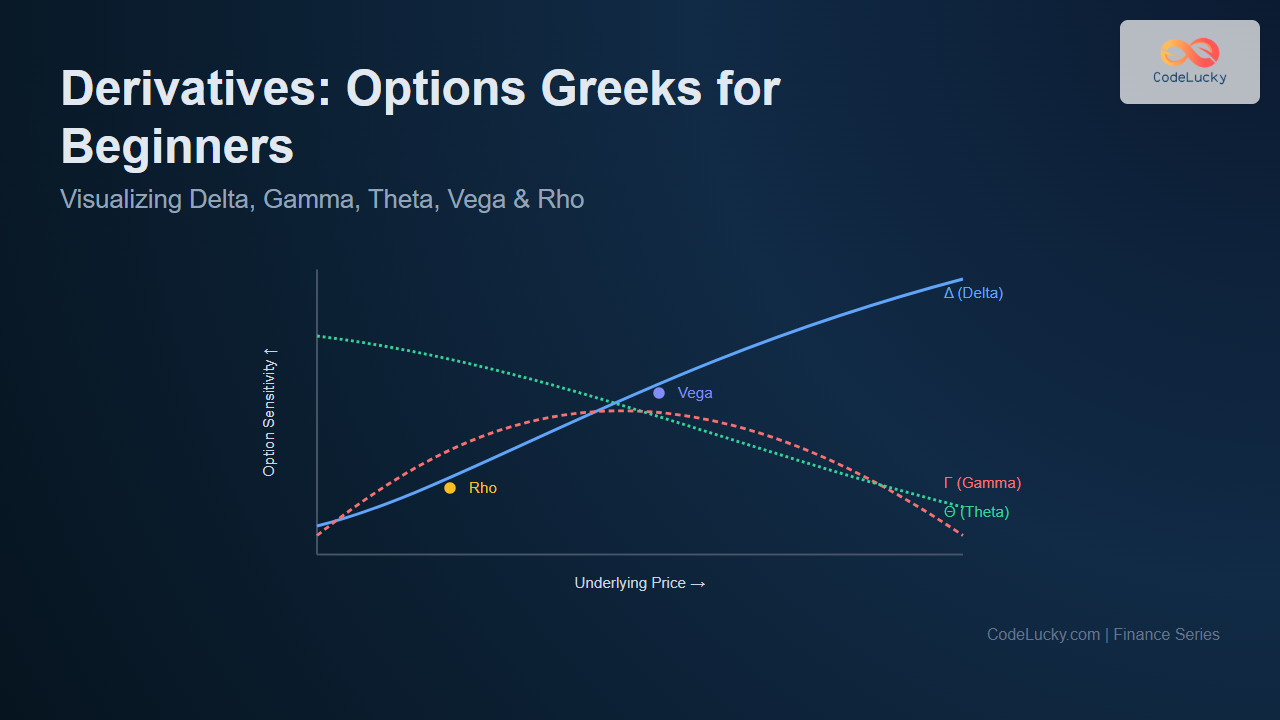
What Are Options Greeks?

Options Greeks are mathematical measures showing how an option’s price responds to different factors. Each Greek represents a distinct type of sensitivity — much like how a car’s dashboard gives readings for speed, fuel, and temperature.

The primary Greeks most traders watch are:

• Delta — Measures price sensitivity to underlying asset changes.
• Gamma — Measures how Delta changes with price movements.
• Theta — Measures time decay as expiration approaches.
• Vega — Measures sensitivity to volatility changes.
• Rho — Measures impact of interest rate changes.

1. Delta – The Directional Sensitivity

Delta measures how much the price of an option changes for a one-point move in the underlying asset. It’s expressed between -1 and +1 (or -100 to +100 for easier comparison).

• For a call option, Delta ranges from 0 to +1.
• For a put option, Delta ranges from 0 to -1.

Example: Suppose you hold a call option with a Delta of 0.60. If the stock price increases by ₹10, the option’s price increases by ₹6.

Delta also helps you assess directional bias. A Delta of 0.5 means the option roughly behaves like owning half of the underlying stock.

Interactive Thought Example

Try adjusting the underlying stock value in your spreadsheet or trading simulator and see how option value moves — you will notice Delta gives a consistent approximation of this movement.

2. Gamma – Delta’s Accelerator

Gamma measures the rate at which Delta changes as the underlying price moves. When price shifts significantly, Delta doesn’t stay constant — Gamma quantifies that sensitivity.

• High Gamma occurs for near-the-money options.
• Low Gamma occurs for deep-in or deep-out of the money options.

Example: If Delta moves from 0.5 to 0.6 after a ₹5 price increase, the Gamma would be (0.1 ÷ 5) = 0.02.

3. Theta – The Time Decay Factor

Theta indicates how much an option’s value decreases with each passing day, assuming all else remains constant. It’s generally negative for both call and put options because time works against option holders.

Example: If Θ = -0.05, the option loses ₹0.05 in value daily due to time decay.

Traders often visualize Theta as a slope — it becomes steeper as expiration nears.

4. Vega – Volatility’s Influence

Vega measures how much an option’s price changes with a 1% change in the underlying’s implied volatility.

Example: If Vega = 0.10, and volatility rises by 5%, the option’s price increases by ₹0.50 (5 × 0.10).

This makes Vega extremely important around events like earnings announcements, when volatility expectations can shift quickly.

5. Rho – The Interest Rate Sensitivity

Rho represents how much an option’s price changes when interest rates move by 1%. Although often smaller than other Greeks, Rho becomes relevant in long-term options or high-rate environments.

Example: A call option with Rho = 0.04 will gain ₹0.04 if interest rates increase by 1%.

Combined View: How Greeks Work Together

Each Greek doesn’t work in isolation. Understanding their interplay helps traders balance portfolios effectively. For example, while Delta tracks direction, Theta tracks time decay and Vega reflects volatility exposure.

Practical Use of Greeks – A Realistic Example

Imagine a trader buying a call option on Nifty50:

Underlying: ₹22,000
Strike Price: ₹22,500
Premium: ₹150
Greeks: Δ=0.40, Γ=0.02, Θ=-0.10, Vega=0.12, Rho=0.03

If the index moves to ₹22,100, option value changes approximately:

• Price effect: 100 × 0.40 = ₹40 increase.
• Time decay: loses ₹10/day (Theta).
• Volatility effect: if volatility rises 5%, adds 5×0.12=₹0.60 gain.

Net effect: Option price ≈ ₹150 + ₹40 – ₹10 + ₹0.60 = ₹180.6

Why Greeks Matter to Beginners

Beginners often mistake options as simple leveraged bets. Greeks reveal the underlying behavior — how multiple forces shape profit and loss. They also guide hedging:

• Delta hedging neutralizes price risk.
• Gamma monitoring ensures stable exposure across strikes.
• Theta management helps time entries near expiration.

Interactive Learning Recommendation

Use any options simulation platform to adjust parameters interactively. Observe:

• How Delta increases as price rises.
• How Theta accelerates as expiry nears.
• How Vega spikes with volatility news.

This hands-on approach solidifies comprehension better than theory alone.

Final Words

Understanding Options Greeks gives you a trader’s edge. Think of them as diagnostic tools that turn guesswork into structured decision-making. Mastering Delta through Rho builds your foundation for more complex strategies such as spreads, straddles, and hedges.

Now that you understand the Greeks, explore how to integrate them into trading systems with our upcoming guide: “Options Strategies Using Greeks.”