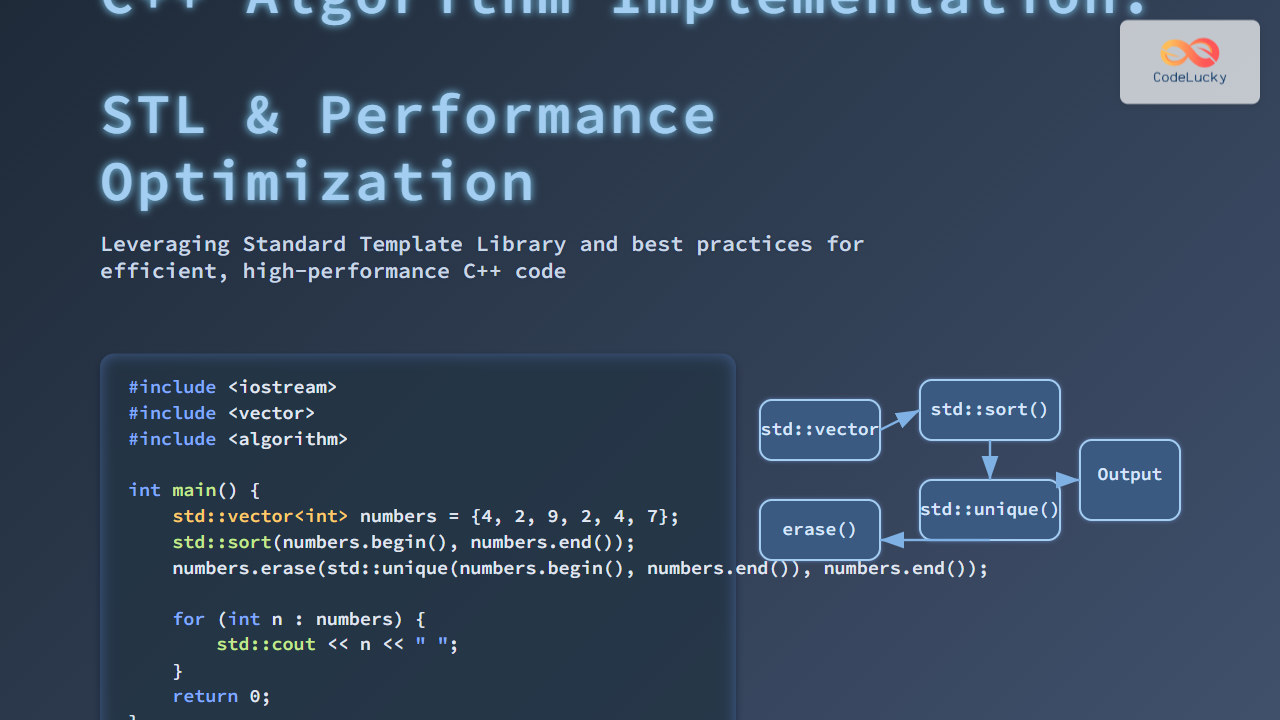
C++ offers a powerful set of algorithms in its Standard Template Library (STL) that can significantly simplify and optimize your code. These algorithms provide efficient, tested, and reusable solutions for common programming tasks. In this comprehensive guide, we'll explore the most important STL algorithms, their usage, and practical examples to help you leverage their power in your C++ projects.
Introduction to STL Algorithms
The C++ Standard Template Library (STL) provides a collection of powerful algorithms that operate on containers and other sequences. These algorithms are function templates that can work with different types of data structures, making them highly versatile and reusable.
🔑 Key benefits of using STL algorithms:
- Improved code readability
- Increased efficiency
- Reduced chances of errors
- Better maintainability
To use STL algorithms, you need to include the <algorithm> header in your C++ program:
#include <algorithm>
Let's dive into some of the most commonly used STL algorithms and see how they can be applied in real-world scenarios.
Sorting Algorithms
std::sort
The std::sort algorithm is one of the most frequently used STL algorithms. It sorts elements in a container in ascending order by default.
#include <iostream>
#include <vector>
#include <algorithm>
int main() {
std::vector<int> numbers = {5, 2, 8, 1, 9, 3, 7, 4, 6};
std::sort(numbers.begin(), numbers.end());
std::cout << "Sorted numbers: ";
for (int num : numbers) {
std::cout << num << " ";
}
std::cout << std::endl;
return 0;
}
Output:
Sorted numbers: 1 2 3 4 5 6 7 8 9
💡 You can also use a custom comparison function to sort in descending order or based on specific criteria:
bool descending(int a, int b) {
return a > b;
}
std::sort(numbers.begin(), numbers.end(), descending);
std::partial_sort
The std::partial_sort algorithm sorts a specified number of elements in a range, leaving the rest unsorted.
#include <iostream>
#include <vector>
#include <algorithm>
int main() {
std::vector<int> numbers = {5, 2, 8, 1, 9, 3, 7, 4, 6};
std::partial_sort(numbers.begin(), numbers.begin() + 4, numbers.end());
std::cout << "Partially sorted numbers: ";
for (int num : numbers) {
std::cout << num << " ";
}
std::cout << std::endl;
return 0;
}
Output:
Partially sorted numbers: 1 2 3 4 9 8 7 5 6
Searching Algorithms
std::find
The std::find algorithm searches for a specific element in a container and returns an iterator to the first occurrence of the element.
#include <iostream>
#include <vector>
#include <algorithm>
int main() {
std::vector<int> numbers = {5, 2, 8, 1, 9, 3, 7, 4, 6};
auto it = std::find(numbers.begin(), numbers.end(), 7);
if (it != numbers.end()) {
std::cout << "Found 7 at position: " << std::distance(numbers.begin(), it) << std::endl;
} else {
std::cout << "7 not found in the vector" << std::endl;
}
return 0;
}
Output:
Found 7 at position: 6
std::binary_search
The std::binary_search algorithm performs a binary search on a sorted range and returns a boolean indicating whether the element is present.
#include <iostream>
#include <vector>
#include <algorithm>
int main() {
std::vector<int> numbers = {1, 2, 3, 4, 5, 6, 7, 8, 9};
bool found = std::binary_search(numbers.begin(), numbers.end(), 5);
std::cout << "Is 5 present in the vector? " << (found ? "Yes" : "No") << std::endl;
return 0;
}
Output:
Is 5 present in the vector? Yes
⚠️ Note: The container must be sorted for std::binary_search to work correctly.
Modifying Algorithms
std::transform
The std::transform algorithm applies a given function to a range of elements and stores the result in another range.
#include <iostream>
#include <vector>
#include <algorithm>
int square(int x) {
return x * x;
}
int main() {
std::vector<int> numbers = {1, 2, 3, 4, 5};
std::vector<int> squared(numbers.size());
std::transform(numbers.begin(), numbers.end(), squared.begin(), square);
std::cout << "Squared numbers: ";
for (int num : squared) {
std::cout << num << " ";
}
std::cout << std::endl;
return 0;
}
Output:
Squared numbers: 1 4 9 16 25
std::replace
The std::replace algorithm replaces all occurrences of a specified value with another value in a given range.
#include <iostream>
#include <vector>
#include <algorithm>
int main() {
std::vector<int> numbers = {1, 2, 3, 2, 4, 2, 5};
std::replace(numbers.begin(), numbers.end(), 2, 10);
std::cout << "Numbers after replacement: ";
for (int num : numbers) {
std::cout << num << " ";
}
std::cout << std::endl;
return 0;
}
Output:
Numbers after replacement: 1 10 3 10 4 10 5
Numeric Algorithms
std::accumulate
The std::accumulate algorithm computes the sum of a range of elements.
#include <iostream>
#include <vector>
#include <numeric>
int main() {
std::vector<int> numbers = {1, 2, 3, 4, 5};
int sum = std::accumulate(numbers.begin(), numbers.end(), 0);
std::cout << "Sum of numbers: " << sum << std::endl;
return 0;
}
Output:
Sum of numbers: 15
💡 You can also use a custom binary operation with std::accumulate:
int product = std::accumulate(numbers.begin(), numbers.end(), 1, std::multiplies<int>());
std::inner_product
The std::inner_product algorithm computes the inner product of two ranges of elements.
#include <iostream>
#include <vector>
#include <numeric>
int main() {
std::vector<int> v1 = {1, 2, 3, 4, 5};
std::vector<int> v2 = {5, 4, 3, 2, 1};
int result = std::inner_product(v1.begin(), v1.end(), v2.begin(), 0);
std::cout << "Inner product: " << result << std::endl;
return 0;
}
Output:
Inner product: 35
Set Algorithms
std::set_intersection
The std::set_intersection algorithm computes the intersection of two sorted ranges.
#include <iostream>
#include <vector>
#include <algorithm>
int main() {
std::vector<int> set1 = {1, 2, 3, 4, 5};
std::vector<int> set2 = {3, 4, 5, 6, 7};
std::vector<int> result;
std::set_intersection(set1.begin(), set1.end(), set2.begin(), set2.end(), std::back_inserter(result));
std::cout << "Intersection: ";
for (int num : result) {
std::cout << num << " ";
}
std::cout << std::endl;
return 0;
}
Output:
Intersection: 3 4 5
std::set_union
The std::set_union algorithm computes the union of two sorted ranges.
#include <iostream>
#include <vector>
#include <algorithm>
int main() {
std::vector<int> set1 = {1, 2, 3, 4, 5};
std::vector<int> set2 = {3, 4, 5, 6, 7};
std::vector<int> result;
std::set_union(set1.begin(), set1.end(), set2.begin(), set2.end(), std::back_inserter(result));
std::cout << "Union: ";
for (int num : result) {
std::cout << num << " ";
}
std::cout << std::endl;
return 0;
}
Output:
Union: 1 2 3 4 5 6 7
Heap Algorithms
std::make_heap
The std::make_heap algorithm converts a range of elements into a heap.
#include <iostream>
#include <vector>
#include <algorithm>
int main() {
std::vector<int> numbers = {3, 1, 4, 1, 5, 9, 2, 6};
std::make_heap(numbers.begin(), numbers.end());
std::cout << "Heap: ";
for (int num : numbers) {
std::cout << num << " ";
}
std::cout << std::endl;
return 0;
}
Output:
Heap: 9 6 4 2 5 1 3 1
std::push_heap and std::pop_heap
The std::push_heap algorithm adds an element to a heap, while std::pop_heap removes the top element from a heap.
#include <iostream>
#include <vector>
#include <algorithm>
int main() {
std::vector<int> numbers = {3, 1, 4, 1, 5, 9, 2, 6};
std::make_heap(numbers.begin(), numbers.end());
numbers.push_back(7);
std::push_heap(numbers.begin(), numbers.end());
std::cout << "Heap after push: ";
for (int num : numbers) {
std::cout << num << " ";
}
std::cout << std::endl;
std::pop_heap(numbers.begin(), numbers.end());
int top = numbers.back();
numbers.pop_back();
std::cout << "Top element: " << top << std::endl;
std::cout << "Heap after pop: ";
for (int num : numbers) {
std::cout << num << " ";
}
std::cout << std::endl;
return 0;
}
Output:
Heap after push: 9 7 4 6 5 1 3 1 2
Top element: 9
Heap after pop: 7 6 4 2 5 1 3 1
Permutation Algorithms
std::next_permutation
The std::next_permutation algorithm generates the next lexicographically greater permutation of a range of elements.
#include <iostream>
#include <vector>
#include <algorithm>
int main() {
std::vector<int> numbers = {1, 2, 3};
do {
for (int num : numbers) {
std::cout << num << " ";
}
std::cout << std::endl;
} while (std::next_permutation(numbers.begin(), numbers.end()));
return 0;
}
Output:
1 2 3
1 3 2
2 1 3
2 3 1
3 1 2
3 2 1
Conclusion
The C++ Standard Template Library provides a rich set of algorithms that can significantly simplify your code and improve its efficiency. By leveraging these algorithms, you can write more concise, readable, and maintainable code.
In this article, we've explored some of the most commonly used STL algorithms, including sorting, searching, modifying, numeric, set, heap, and permutation algorithms. Each of these algorithms comes with its own set of use cases and can be incredibly powerful when applied correctly.
🚀 Key takeaways:
- STL algorithms work with different container types, making them highly versatile.
- They often provide better performance than hand-written loops.
- Using STL algorithms can lead to fewer bugs and more maintainable code.
- Many algorithms allow for customization through function objects or lambda expressions.
As you continue to develop your C++ skills, make it a habit to reach for these standard library algorithms before implementing your own solutions. They're well-tested, efficient, and can save you significant development time.
Remember, the examples provided here are just the tip of the iceberg. The C++ Standard Library offers many more algorithms that can help you solve a wide range of programming problems. Always refer to the official C++ documentation for the most up-to-date and comprehensive information on these algorithms.
Happy coding, and may your C++ journey be filled with efficient algorithms and elegant solutions! 🖥️💻🔍