The Traveling Salesman Problem (TSP) is one of the most famous and challenging problems in computer science, combinatorial optimization, and operations research. It belongs to the class of NP-Hard problems, meaning no known polynomial-time solution can solve all instances efficiently. This article explores the core concepts behind TSP, why it is so notoriously difficult, and popular approaches to finding approximate solutions, complete with rich visualizations and examples to clarify the concepts for enthusiasts and professionals alike.
What is the Traveling Salesman Problem?
The Traveling Salesman Problem asks the question: Given a list of cities and the distances between each pair of cities, what is the shortest possible route that visits each city exactly once and returns to the origin city? Formally, it is a problem defined on a weighted complete graph where nodes represent cities and edges represent travel cost or distance between cities.
Finding the shortest path that covers all these nodes once and returns to the start is the core challenge.
Why is TSP NP-Hard?
The TSP is classified as NP-Hard because it is computationally intensive to solve exactly as the number of cities increases. The number of possible routes grows factorially: for n cities, there are (n-1)! / 2 possible unique routes (considering round trips and ignoring direction). For example, with 10 cities, there are over 180,000 possible routes to consider.
This factorial explosion means the problem quickly becomes infeasible to solve via brute force for even moderately large instances. Since no known polynomial-time algorithm exists for solving all cases optimally, it is used as a benchmark for computational complexity and approximation algorithms.
Classic Examples of TSP
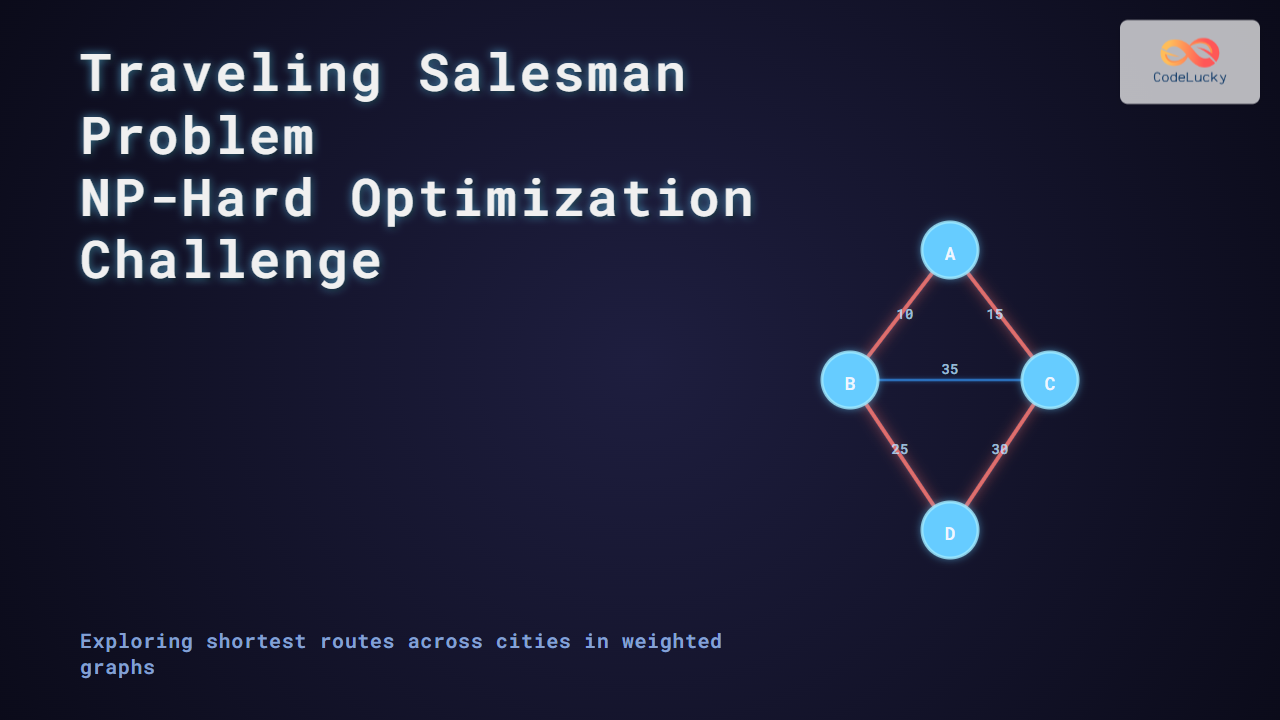
Consider 4 cities with the following distances (in kilometers):
| From | To | Distance |
|---|---|---|
| A | B | 10 |
| A | C | 15 |
| A | D | 20 |
| B | C | 35 |
| B | D | 25 |
| C | D | 30 |
The goal is to find the route that visits A, B, C, and D exactly once and returns to A, minimizing total distance.
Possible routes and distances:
- A → B → C → D → A = 10 + 35 + 30 + 20 = 95
- A → B → D → C → A = 10 + 25 + 30 + 15 = 80
- A → C → B → D → A = 15 + 35 + 25 + 20 = 95
- A → C → D → B → A = 15 + 30 + 25 + 10 = 80
- A → D → B → C → A = 20 + 25 + 35 + 15 = 95
- A → D → C → B → A = 20 + 30 + 35 + 10 = 95
The optimal solutions here are routes with distance 80.
Popular Algorithms and Approaches
Since solving TSP exactly is computationally hard for large inputs, several algorithms and heuristics are used:
Exact Algorithms
- Brute Force: Checks all permutations to find the minimum route; limited to very small datasets.
- Dynamic Programming (Held-Karp Algorithm): Uses memoization to reduce complexity to O(n²2ⁿ), still expensive for large n.
- Integer Linear Programming (ILP): Models TSP as ILP and solves using solvers like CPLEX or Gurobi.
Heuristic and Approximation Algorithms
- Nearest Neighbor: Greedy approach picking the nearest unvisited city; fast but not always optimal.
- Christofides’ Algorithm: Guarantees route within 1.5 times the optimal for symmetric TSP.
- Genetic Algorithms, Simulated Annealing, Ant Colony Optimization: Metaheuristics that provide good solutions with reasonable resource use.
Visual Example of Nearest Neighbor Heuristic
Starting at City A, the algorithm chooses the nearest unvisited city iteratively:
Route: A → B → D → C → A
Interactive Visualization Concept
Imagine an interactive interface where a user places cities on a map, and the algorithm dynamically calculates routes using heuristics or exact methods. This tool helps understand TSP dynamics in real-time.
For HTML/JS integration, one could implement with canvas and JavaScript, showcasing path costs updating as cities are moved or algorithms run stepwise.
Why Study TSP?
Beyond being a classic problem for computational theory, TSP has practical applications in logistics, manufacturing, DNA sequencing, and even robotics. Its study advances research in optimization, complexity theory, and algorithmic design.
Summary
The Traveling Salesman Problem is a cornerstone problem illustrating the challenges of NP-Hard optimization tasks. Though exact solutions are costly for large instances, numerous heuristic and approximation approaches provide practical answers for real-world scenarios. Understanding TSP fosters deeper insights into algorithm design and computational complexity.