Topological Sort: Linear Ordering of Directed Acyclic Graph Explained with Examples

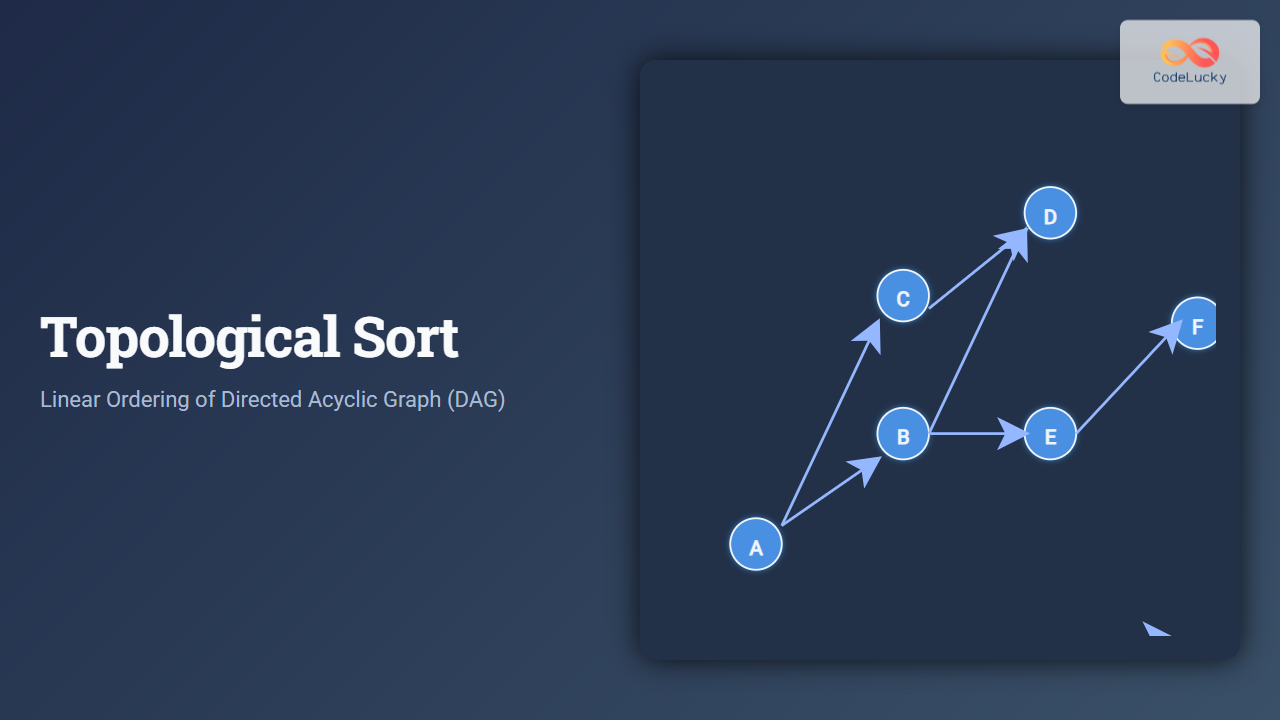
In graph theory, Topological Sort is a fundamental algorithm used to linearly order the vertices of a Directed Acyclic Graph (DAG). Unlike traditional sorting, topological sorting applies only to directed graphs without cycles, arranging the nodes such that every directed edge u → v implies that u comes before v in the ordering.

This concept plays a central role in real-world applications such as:

• Task Scheduling: Determining order of execution where tasks depend on each other.
• Compilation Order: Sorting source files so dependencies compile first.
• Course Prerequisite Planning: Arranging courses based on prerequisite structure.
• Build Systems: Deciding order of linking or builds in DevOps pipelines.

What is Topological Sort?

A topological sort of a DAG is a linear ordering of its vertices such that:

• Every directed edge (u → v) places u before v.
• If the graph contains a cycle, no valid topological ordering is possible.

For the graph above, one valid topological order is: A → B → C → D. Another possible order is A → C → B → D. Multiple valid orders may exist, as long as dependencies are maintained.

Algorithms for Topological Sort

There are two popular approaches to compute topological ordering of a DAG:

1. Depth-First Search (DFS) Based Approach
2. Kahn’s Algorithm (BFS Based)

1. DFS Based Topological Sort

The strategy is to explore nodes recursively and push them onto a stack after visiting all their descendants. Reversing the stack yields a valid topological ordering.

from collections import defaultdict

def dfs_topological_sort(vertices, edges):
    graph = defaultdict(list)
    for u, v in edges:
        graph[u].append(v)

    visited = set()
    stack = []

    def dfs(node):
        visited.add(node)
        for neighbor in graph[node]:
            if neighbor not in visited:
                dfs(neighbor)
        stack.append(node)

    for v in vertices:
        if v not in visited:
            dfs(v)

    return stack[::-1]

# Example
vertices = ['A', 'B', 'C', 'D']
edges = [('A', 'B'), ('A', 'C'), ('B', 'D'), ('C', 'D')]

order = dfs_topological_sort(vertices, edges)
print("Topological Order:", order)

Output:

Topological Order: ['A', 'C', 'B', 'D']

Explanation: A comes first as it has no prerequisites, then C or B, and finally D after both are placed before it.

2. Kahn’s Algorithm (BFS Based)

Kahn’s algorithm builds the order iteratively by removing nodes of in-degree 0 (no incoming edges). Each removal also decreases in-degree of neighbors.

from collections import defaultdict, deque

def kahn_topological_sort(vertices, edges):
    graph = defaultdict(list)
    indegree = {v: 0 for v in vertices}

    for u, v in edges:
        graph[u].append(v)
        indegree[v] += 1

    queue = deque([v for v in vertices if indegree[v] == 0])
    topo_order = []

    while queue:
        node = queue.popleft()
        topo_order.append(node)
        for neighbor in graph[node]:
            indegree[neighbor] -= 1
            if indegree[neighbor] == 0:
                queue.append(neighbor)

    if len(topo_order) == len(vertices):
        return topo_order
    else:
        raise ValueError("Graph has a cycle, topological sort not possible")

# Example
vertices = ['A', 'B', 'C', 'D']
edges = [('A', 'B'), ('A', 'C'), ('B', 'D'), ('C', 'D')]

order = kahn_topological_sort(vertices, edges)
print("Topological Order:", order)

Output:

Topological Order: ['A', 'B', 'C', 'D']

Visualizing Kahn’s Algorithm – Step by Step

Steps:

1. Start with indegree = 0 nodes: [A]
2. Remove A, add B and C when their indegree drops to 0.
3. Process B and C, then D becomes available.
4. Final order: A → B → C → D

Complexity Analysis

• Time Complexity: O(V + E), where V = vertices, E = edges.
• Space Complexity: O(V) for maintaining visited, indegree, and stack/queue.

Applications of Topological Sorting

• Course Prerequisites: Determining feasible learning paths.
• Build Systems: Deciding compilation and linking order of modules like in Makefiles.
• Task Scheduling: Scheduling jobs in operating systems or distributed computation.
• Language Parsing: Resolving symbol dependencies in compilers.

Conclusion

Topological Sort provides a powerful mechanism to order tasks, courses, or compilation units where dependencies exist. Its importance lies in breaking down directed acyclic graphs into a linear representation. Both DFS-based approach and Kahn’s Algorithm are efficient and widely used in industry-level applications.

If your graph contains cycles, remember: No topological ordering exists. Detecting cycles as part of these algorithms ensures correctness when solving real-world dependency problems.