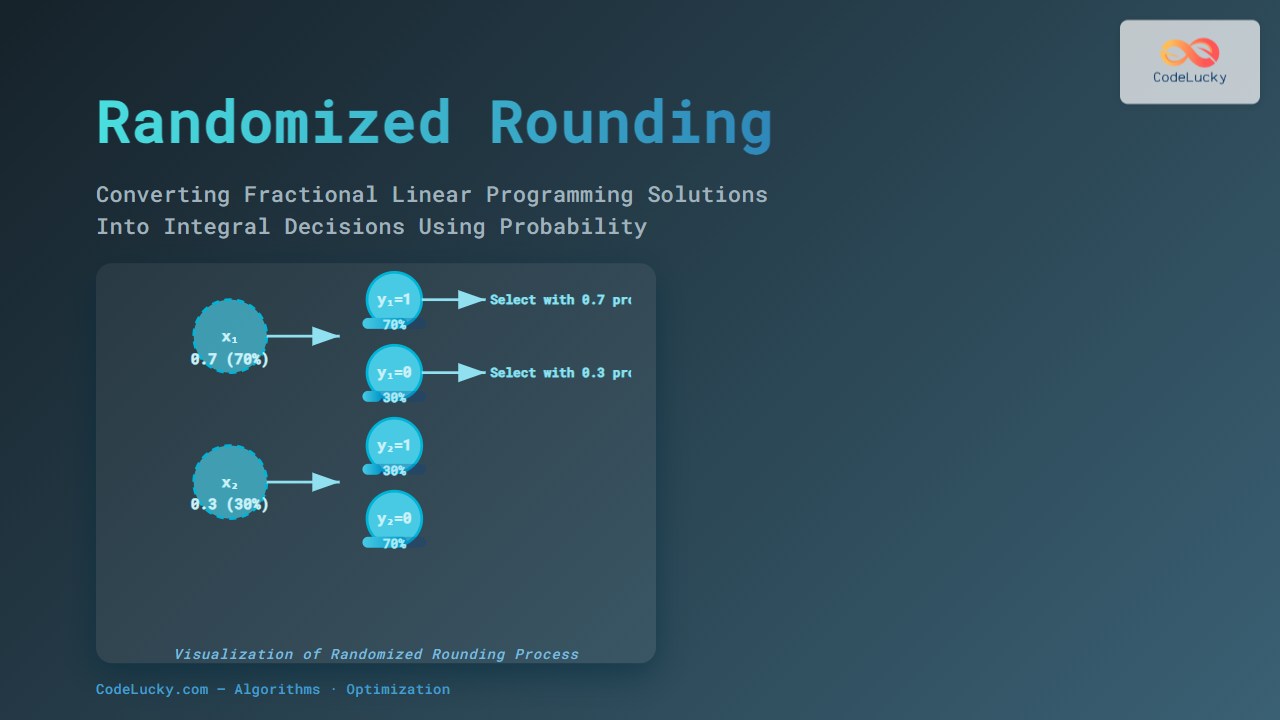
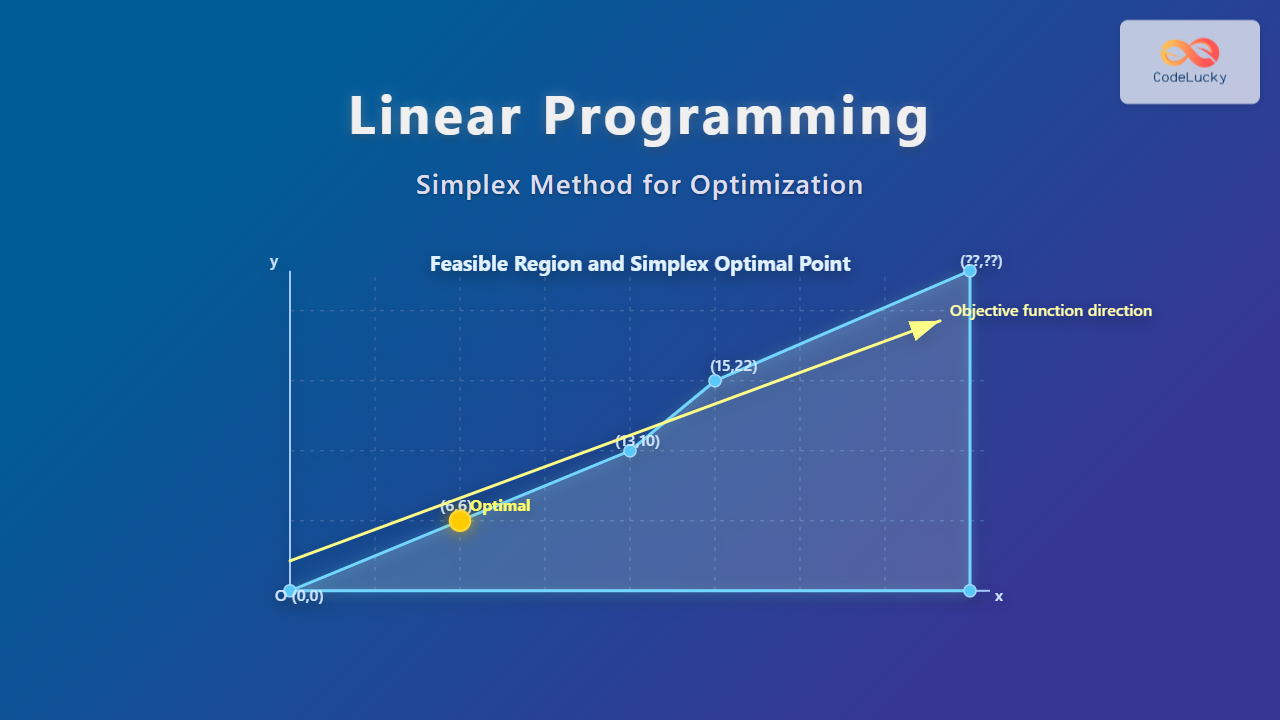
Optimization problems are common across many computer science and engineering fields, where the goal is to find the best solution among many possible candidates. However, many traditional search methods can get trapped in local optima, which are suboptimal solutions better than their neighbors but not the best globally.
Tabu Search is a powerful metaheuristic algorithm designed specifically to overcome this limitation, enabling exploration beyond local optima by intelligently guiding the search process. This article delivers a comprehensive understanding of Tabu Search, detailed examples with clear visual outputs, and mermaid diagrams that clarify its workings.
What is Tabu Search?
Tabu Search, introduced by Fred Glover in 1986, is a metaheuristic that guides a local search procedure to explore the solution space beyond local optimality. It does so by maintaining a flexible memory structure called a Tabu List that temporarily forbids or penalizes moves that would take the search back to recently visited solutions, thereby encouraging exploration of new regions in the search space.
Unlike simple local search methods that move only to better neighbors, Tabu Search allows moves that do not improve the solution, thus escaping local optima traps.
Core Concepts of Tabu Search
- Initial Solution: The algorithm starts from an initial feasible solution, which can be generated randomly or by a heuristic.
- Neighborhood Structure: Defines all solutions reachable by a simple modification of the current solution (e.g., swapping two elements, changing a variable).
- Tabu List: A short-term memory storing recent moves or attributes that are forbidden for a certain number of iterations (Tabu tenure) to avoid cycles.
- Aspiration Criteria: Override the Tabu status if a move yields a solution better than any previously found.
- Stopping Criteria: Could be a fixed number of iterations, time limit, or convergence.
How Tabu Search Works: Step-by-Step
1. Initialization: Start with an initial solution and initialize the Tabu list as empty.
2. Neighborhood Exploration: Generate neighboring solutions by simple transformations.
3. Move Selection: Select the best candidate not forbidden by the Tabu list or that meets aspiration criteria.
4. Update Tabu List: Record the recent move or solution attributes to forbid cycling back soon.
5. Update Best Solution: If the current solution improves on the best-known, update it.
6. Repeat: Loop until the stopping condition is met.
Example: Tabu Search for the Traveling Salesman Problem (TSP)
Consider the classic optimization problem of TSP, where the goal is to find the shortest possible route visiting every city once and returning to the start.
We begin with an initial route and at each step try to improve it by swapping two cities in the route (a simple neighborhood move). The Tabu list keeps track of recent swaps to prevent undoing the last moves.
Example initial route:
City A → City B → City C → City D → City E → City A
Suppose we swap City B and City D. That swap is recorded as Tabu for the next 5 iterations to avoid reversing it immediately, enabling Tabu Search to explore new routes even if temporarily worse.
Tabu Search Pseudocode
function TabuSearch(initial_solution, max_iterations, tabu_tenure):
current_solution = initial_solution
best_solution = current_solution
tabu_list = empty list
for iteration in 1 to max_iterations:
neighborhood = generate_neighbors(current_solution)
candidate = select_best_candidate(neighborhood, tabu_list, best_solution)
current_solution = candidate.solution
update_tabu_list(tabu_list, candidate.move, tabu_tenure)
if candidate.solution_cost < best_solution_cost:
best_solution = candidate.solution
if stopping_criteria_met():
break
return best_solution
Advantages of Tabu Search
- Efficiently escapes local optima by allowing non-improving moves.
- Flexible with customizable memory structures (Tabu list) and aspiration criteria.
- Widely applicable to many combinatorial optimization problems like scheduling, routing, and resource allocation.
- Balances intensification (deep search nearby) and diversification (broad exploration).
Considerations and Best Practices
- Tabu Tenure Size: Needs tuning; too small risks cycling, too large may over-restrict search.
- Neighborhood Design: Determines search quality and speed; must be problem-specific and efficient.
- Aspiration Criteria: Important to avoid missing promising solutions blocked by Tabu.
- Hybrid Approaches: Often combined with other heuristics or metaheuristics for improved performance.
Interactive Example Walkthrough
Imagine a simple optimization over numeric values aiming to find the minimum of the function f(x) = (x-3)^2 starting from x=0. The neighborhood is defined as allowing steps of ±1.
Tabu Search will explore moves even if temporarily worse, marking recent moves as Tabu to avoid reversing immediately:
- Start at x=0, f(0)=9
- Move to x=1 (f=4), tabu (move x0→x1) recorded
- Move to x=2 (f=1), tabu moves updated
- Move to x=3 (f=0), optimal found
This simple example demonstrates how Tabu Search guides the search towards the global minimum avoiding looping back too quickly.
Summary
Tabu Search is a versatile and robust optimization metaheuristic that plays a crucial role in escaping local optima traps typical of simpler algorithms. With its use of a memory structure (Tabu list) and adaptable search rules, it efficiently balances exploration and exploitation of solution spaces for complex optimization problems.
Its widespread applicability and ease of hybridization with other techniques make it an important algorithm to understand for practitioners tackling diverse computational optimization challenges.