Sweep Line Algorithm: Process Events in Order to Solve Geometric Problems

The Sweep Line Algorithm is a powerful technique used extensively in computational geometry to process geometric events efficiently by sweeping a conceptual line over the plane and handling events in sorted order. This approach transforms complex spatial problems into manageable event-driven processes by leveraging the natural ordering of coordinates or other key attributes. It is particularly useful in problems like finding intersections, closest pairs, or constructing Voronoi diagrams.

Table of Contents

What Is the Sweep Line Algorithm?

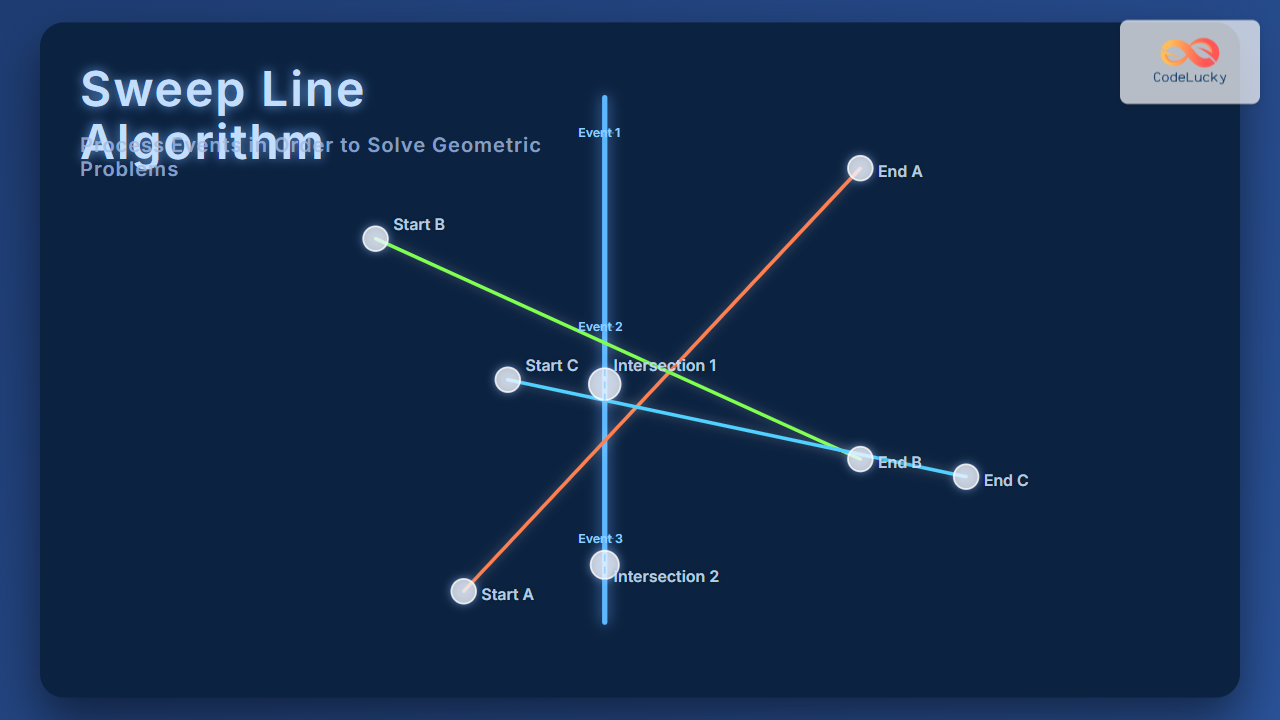
At its core, the Sweep Line Algorithm involves moving a line (usually vertical or horizontal) across the plane from one side to another and processing events at discrete points along this line. These events could be points, segment endpoints, or intersections. By maintaining an active data structure that stores the status of the sweep line, the algorithm efficiently updates and queries geometric configurations as the line advances.

Key Components

Event Points: These are all the discrete points where changes occur (e.g., segment start/end points, intersection points).
Sweep Line Status: A dynamic data structure (often a balanced tree) that maintains all geometric objects intersecting the sweep line at the current position.
Event Queue: A priority queue that holds all upcoming event points, sorted by their coordinate along the sweep direction.

How Sweep Line Algorithm Works

The algorithm generally follows these steps:

Initialize the Event Queue: Insert all starting event points of the problem sorted by their coordinates.
Process Events in Order: Extract the next event from the queue and handle it according to the problem’s rules.
Update Sweep Line Status: Modify the active structure depending on event type (e.g., add or remove segments).
Find New Events: Detect potential new events (like intersections) created by updates and add them to the queue.

Example: Finding Intersections Among Line Segments

One classic use case of the Sweep Line Algorithm is detecting intersections among a set of line segments. The naive approach compares every pair, which can be inefficient with O(n²) complexity. Sweep line reduces this significantly to O((n + k) log n) where k is intersections.

Step-by-Step Example

Input: A set of line segments scattered across the plane.
Process: Sweep from left to right. Insert segment start points in event queue.
When a segment starts, add it to sweep line status sorted by its vertical position.
When a segment ends, remove it and check neighbors for intersections.
When intersections are found, add those event points to the queue.

Visual Output Explanation

Consider three segments crossing:

Vertical sweep line moves from left to right.
Segments enter the sweep line status when their start points are reached.
When sweep reaches an intersection point event, it reorders segments in the status and logs the intersection.
Segments leaving the sweep line status upon their end points are removed.


Sweep Line Position: |      |
Segments Active:       A ----
                      B ----
                      C ----
Events Processed: start_A, start_B, intersection_AB, start_C, end_A, end_B, ...

Interactive Visualization (Conceptual)

Users can imagine a vertical line sweeping across points and segments on a 2D plane, dynamically updating the active set:

The vertical line moves horizontally.
Events trigger updates in the active segment list.
New intersections dynamically appear and are processed in order.

Applications of Sweep Line Algorithm

Line Segment Intersection: Detect all intersections efficiently.
Closest Pair Problems: Reduce comparisons by using a sweep line in one dimension.
Voronoi Diagrams Construction: Key part of Fortune’s sweep-line algorithm.
Polygon Triangulation: Process vertices in an order to decompose polygons efficiently.

Advantages and Limitations

The Sweep Line Algorithm provides an efficient way to handle geometric problems by processing events in a sorted, orderly fashion, avoiding exhaustive comparisons.

However, it requires careful implementation of event handling and balanced data structures, which can be complex.

Conclusion

The Sweep Line Algorithm is an essential paradigm in computational geometry, enabling efficient event-driven solutions for a range of challenging problems. Mastery of this algorithm expands capabilities in graphics, GIS, CAD, and more.