Introduction to Support Vector Machine
Support Vector Machine (SVM) is a powerful supervised learning algorithm widely used for classification and regression tasks in machine learning. The fundamental goal of SVM is to find the best separating hyperplane that maximizes the margin between different classes in the feature space. This article delves into the maximum margin classification concept, providing detailed explanations, practical examples, and visualizations to understand how SVM works under the hood.
What is Maximum Margin Classification?
Maximum margin classification refers to the idea of finding a hyperplane that not only separates the classes but does so with the largest possible margin or gap between the nearest data points from both classes. This greatest margin helps improve the model’s generalization ability by reducing the chance of misclassifying future unseen data.
The Geometry of SVM
Consider a two-dimensional feature space where the classes are linearly separable. The SVM finds a line (in 2D) or hyperplane (in higher dimensions) that separates these classes. The hyperplane is characterized by the equation:
w • x + b = 0
Where w is the weight vector perpendicular to the hyperplane, x is a feature vector, and b is the bias term.
The margin is the distance from this hyperplane to the closest data points of each class, called support vectors. The margin boundaries can be formulated as:
w • x + b = 1 and w • x + b = -1
Maximizing the margin equates to minimizing ||w|| (the norm of the weight vector) subject to the constraint that all points are correctly classified:
y_i (w • x_i + b) ≥ 1, for all i
Mathematical Formulation
The optimization problem for maximum margin classification is:
minimize (1/2) ||w||^2
subject to y_i (w • x_i + b) ≥ 1, ∀ iThis is a convex quadratic programming problem solvable by various algorithms.
Illustrative Example of Maximum Margin Classification
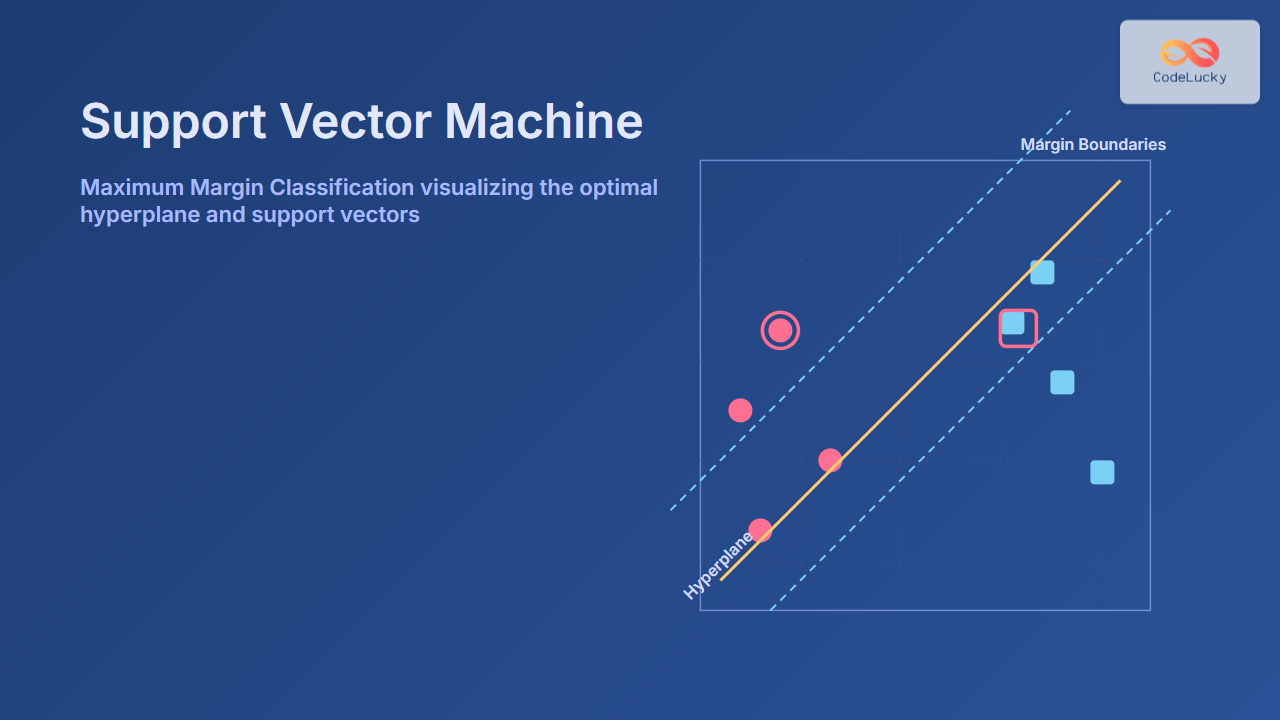
Imagine a simple dataset with two classes (red circles and blue squares) that can be linearly separated.
Visual: Maximum margin hyperplane (green solid) and margin boundaries (dashed green lines) with support vectors nearest to the hyperplane from each class.
Support Vectors – The Key Players
Support vectors are the critical training samples lying exactly on the margin boundaries. They are the data points that determine the position and orientation of the separating hyperplane. Removing or moving other points that are not support vectors does not affect the hyperplane, whereas altering the support vectors can shift the classification boundary.
Interactive Insight: SVM Margin Adjustment
One can imagine interactively moving points in 2D space to observe how the SVM hyperplane and margins adjust. Although this is not executable here, many online SVM interactive demos exist for deep exploration.
Why Maximum Margin? Advantages of SVM
- Better Generalization: By maximizing the margin, SVM tries to minimize classification errors on unseen data.
- Robustness: Only support vectors influence the decision boundary, making the model resistant to outliers far from the margin.
- Convex Optimization: Guarantees a unique and global optimum solution, avoiding local minima.
Conclusion
Support Vector Machine’s maximum margin classification principle is foundational for building efficient classifiers with high prediction accuracy. By focusing on maximizing the gap between classes via the closest data points (support vectors), SVM achieves remarkable robustness and generalization power. Thorough understanding of this concept unlocks applying SVM effectively to diverse classification challenges in real-world machine learning.