Sudoku Solver Algorithm: Backtracking Number Puzzle Solution Explained with Examples

Sudoku is one of the most popular number puzzles in the world. While solving Sudoku by hand requires patience and logical reasoning, computers can approach it using efficient algorithms. Among these, the Backtracking Algorithm is the most widely used for solving Sudoku puzzles programmatically. In this article, we will explain the Sudoku solver algorithm step by step, demonstrate its working with clear examples, and provide a fully functional Python implementation.

What is Sudoku?

Sudoku is a 9×9 grid puzzle divided into 3×3 sub-grids. The goal is to fill the entire grid with numbers 1 through 9 such that:

• Each row contains numbers 1 to 9 without repetition.
• Each column contains numbers 1 to 9 without repetition.
• Each 3×3 subgrid contains numbers 1 to 9 without repetition.

An incomplete Sudoku puzzle usually provides some cells filled with numbers, and the challenge is to fill in the empty cells.

Backtracking Approach for Sudoku Solver

The Backtracking Algorithm is a depth-first search technique where we try filling a number in a cell, and if it leads to a contradiction, we backtrack and try another number. This ensures that we eventually find a valid solution if one exists.

The general algorithm for Sudoku solver is:

1. Find an empty cell.
2. Attempt placing numbers 1 to 9 in the empty cell.
3. Check if placing that number is valid (no repetition in row, column, or subgrid).
4. If valid, recursively attempt to solve the rest of the puzzle.
5. If the attempt fails, backtrack and try a different number.
6. Continue until the entire grid is filled correctly.

Python Implementation of Sudoku Solver

Let’s implement the Sudoku solver in Python using backtracking:

def print_grid(grid):
    for row in grid:
        print(" ".join(str(num) if num != 0 else "." for num in row))

def is_valid(grid, row, col, num):
    # Row check
    if num in grid[row]:
        return False
    
    # Column check
    for r in range(9):
        if grid[r][col] == num:
            return False
    
    # Subgrid check
    start_row, start_col = row - row % 3, col - col % 3
    for r in range(3):
        for c in range(3):
            if grid[start_row + r][start_col + c] == num:
                return False
    
    return True

def solve_sudoku(grid):
    for row in range(9):
        for col in range(9):
            if grid[row][col] == 0:
                for num in range(1, 10):
                    if is_valid(grid, row, col, num):
                        grid[row][col] = num
                        if solve_sudoku(grid):
                            return True
                        grid[row][col] = 0  # Backtrack
                return False
    return True

# Example Sudoku puzzle
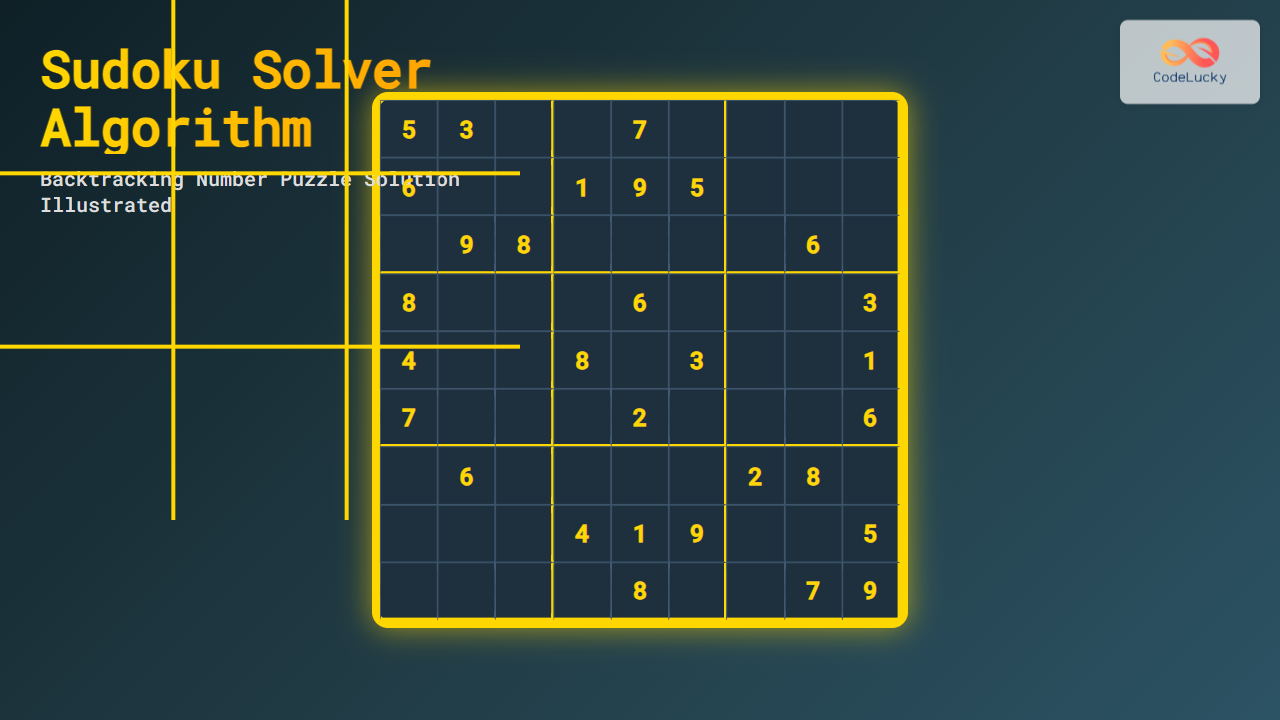
sudoku_grid = [
    [5, 3, 0, 0, 7, 0, 0, 0, 0],
    [6, 0, 0, 1, 9, 5, 0, 0, 0],
    [0, 9, 8, 0, 0, 0, 0, 6, 0],
    [8, 0, 0, 0, 6, 0, 0, 0, 3],
    [4, 0, 0, 8, 0, 3, 0, 0, 1],
    [7, 0, 0, 0, 2, 0, 0, 0, 6],
    [0, 6, 0, 0, 0, 0, 2, 8, 0],
    [0, 0, 0, 4, 1, 9, 0, 0, 5],
    [0, 0, 0, 0, 8, 0, 0, 7, 9]
]

if solve_sudoku(sudoku_grid):
    print_grid(sudoku_grid)
else:
    print("No solution exists")

Example Output

5 3 4 6 7 8 9 1 2
6 7 2 1 9 5 3 4 8
1 9 8 3 4 2 5 6 7
8 5 9 7 6 1 4 2 3
4 2 6 8 5 3 7 9 1
7 1 3 9 2 4 8 5 6
9 6 1 5 3 7 2 8 4
2 8 7 4 1 9 6 3 5
3 4 5 2 8 6 1 7 9

Visualization of Sudoku Solving Process

We can represent how the algorithm explores possibilities and backtracks when necessary:

Time and Space Complexity

The Sudoku solver using backtracking has significant computational cost.

• Time Complexity: In the worst case, it is O(9^(n*n)) for an n x n board (for Sudoku, 9×9). However, due to constraints and pruning, it solves practical puzzles fast.
• Space Complexity: O(n*n) for storing the board and recursive call stack.

Interactive Idea for Learning

If implemented in a web environment (JavaScript + HTML5 Canvas), you can create an interactive Sudoku solver that visually places numbers on the grid step by step. Each backtracking step can be animated to help learners visualize the algorithm.

Conclusion

The Sudoku Solver Algorithm using Backtracking is a powerful example of recursion and constraint satisfaction. While inefficient in brute force search for general problems, it is highly effective for Sudoku puzzles because of built-in logical constraints. By understanding this algorithm, programmers can strengthen their grasp of recursion, backtracking, and problem-solving techniques applicable to many constraint satisfaction problems beyond Sudoku.