In graph theory, a Strongly Connected Component (SCC) is a maximal subgraph of a directed graph in which every vertex is reachable from every other vertex inside that subgraph. SCCs play a crucial role in analyzing dependencies, detecting cycles, and optimizing computations in directed graphs.
Two popular algorithms for finding SCCs are Tarjan’s Algorithm and Kosaraju’s Algorithm. Both are efficient and widely used in applications such as compiler design, deadlock detection, and social network analysis.
Understanding Strongly Connected Components
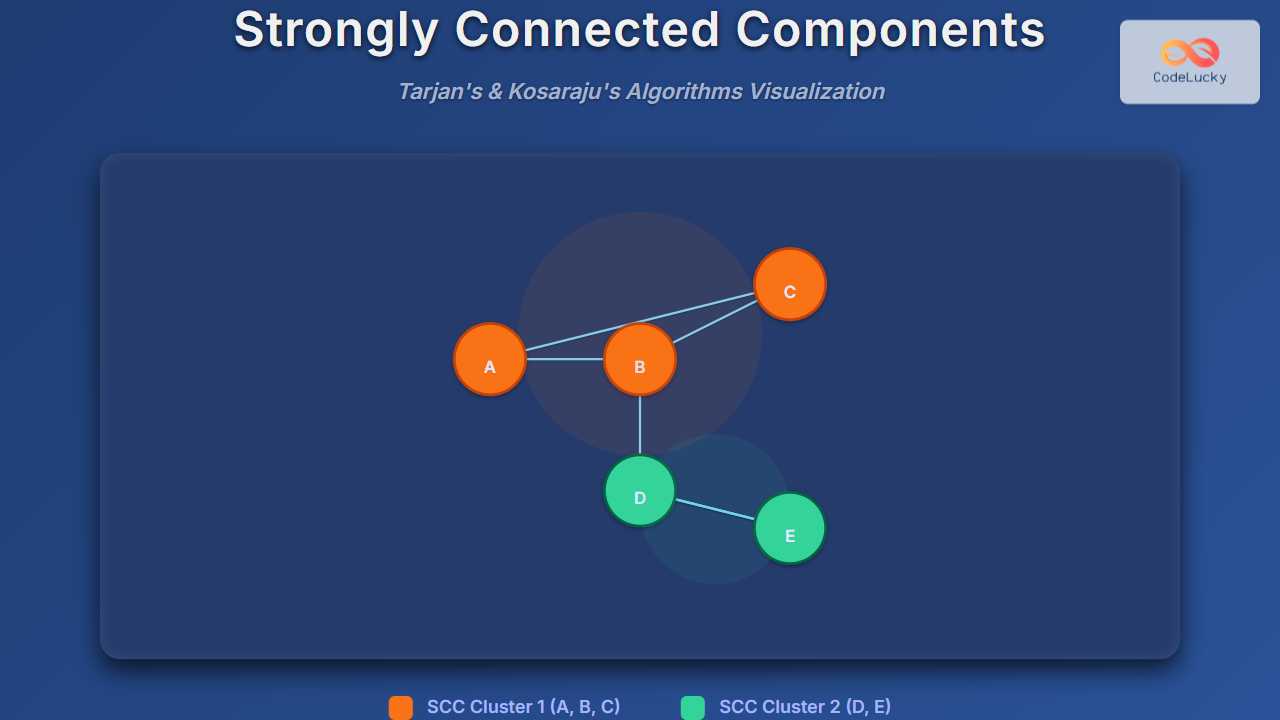
To understand SCCs, consider a directed graph where edges have directions. Nodes form an SCC if each node can reach every other node in the group through directed paths. For example, if node A can reach B, B can reach C, and C can reach A, then {A, B, C} is a strongly connected component.
In the above graph, {A, B, C} forms one SCC and {D, E} forms another. Node sets like these partition the graph into disjoint strongly connected components.
Kosaraju’s Algorithm
Kosaraju’s Algorithm finds SCCs using two Depth-First Searches (DFS). The steps are:
- Perform DFS on the original graph and push nodes into a stack in finishing order (when DFS backtracks).
- Reverse all graph edges to create a transpose graph.
- Perform DFS in the order of nodes popped from the stack on the transposed graph. Each DFS tree gives one Strongly Connected Component.
Kosaraju’s Algorithm Example in Python
from collections import defaultdict
class Graph:
def __init__(self, n):
self.n = n
self.graph = defaultdict(list)
def add_edge(self, u, v):
self.graph[u].append(v)
def dfs(self, v, visited, stack=None, collect=None):
visited[v] = True
if collect is not None:
collect.append(v)
for nei in self.graph[v]:
if not visited[nei]:
self.dfs(nei, visited, stack, collect)
if stack is not None:
stack.append(v)
def transpose(self):
g = Graph(self.n)
for u in self.graph:
for v in self.graph[u]:
g.add_edge(v, u)
return g
def kosaraju(self):
stack = []
visited = [False]*self.n
for v in range(self.n):
if not visited[v]:
self.dfs(v, visited, stack)
gT = self.transpose()
visited = [False]*self.n
scc = []
while stack:
v = stack.pop()
if not visited[v]:
component = []
gT.dfs(v, visited, collect=component)
scc.append(component)
return scc
g = Graph(5)
g.add_edge(0, 1)
g.add_edge(1, 2)
g.add_edge(2, 0)
g.add_edge(1, 3)
g.add_edge(3, 4)
g.add_edge(4, 3)
print("SCCs (Kosaraju):", g.kosaraju())
This will output SCCs such as [[0, 2, 1], [3, 4]], confirming the decomposition into two strongly connected components.
Tarjan’s Algorithm
Tarjan’s Algorithm is a single-pass DFS-based algorithm that finds SCCs using concepts of low-link values. It avoids building a transpose graph, making it slightly more efficient in practice.
The key ideas are:
- Assign each node an index during DFS traversal.
- Maintain a low-link value: the smallest index reachable from that node through DFS tree or back edges.
- Use a stack to track the current DFS path. When a node’s index equals its low-link value, it becomes the root of an SCC and all nodes up to it on the stack form one strongly connected component.
Tarjan’s Algorithm Implementation in Python
class TarjanSCC:
def __init__(self, n):
self.graph = defaultdict(list)
self.n = n
self.index = 0
self.stack = []
self.on_stack = [False]*n
self.indices = [-1]*n
self.low = [-1]*n
self.sccs = []
def add_edge(self, u, v):
self.graph[u].append(v)
def strongconnect(self, v):
self.indices[v] = self.index
self.low[v] = self.index
self.index += 1
self.stack.append(v)
self.on_stack[v] = True
for w in self.graph[v]:
if self.indices[w] == -1:
self.strongconnect(w)
self.low[v] = min(self.low[v], self.low[w])
elif self.on_stack[w]:
self.low[v] = min(self.low[v], self.indices[w])
if self.low[v] == self.indices[v]:
comp = []
while True:
w = self.stack.pop()
self.on_stack[w] = False
comp.append(w)
if w == v:
break
self.sccs.append(comp)
def tarjan(self):
for v in range(self.n):
if self.indices[v] == -1:
self.strongconnect(v)
return self.sccs
tg = TarjanSCC(5)
tg.add_edge(0, 1)
tg.add_edge(1, 2)
tg.add_edge(2, 0)
tg.add_edge(1, 3)
tg.add_edge(3, 4)
tg.add_edge(4, 3)
print("SCCs (Tarjan):", tg.tarjan())
This produces the same result as Kosaraju’s algorithm, for example: [[2, 1, 0], [4, 3]].
Comparison Between Tarjan’s and Kosaraju’s Algorithms
| Aspect | Kosaraju’s Algorithm | Tarjan’s Algorithm |
|---|---|---|
| DFS Passes | Two DFS traversals (original and transposed graph) | One DFS traversal |
| Complexity | O(V + E) | O(V + E) |
| Ease of Understanding | Conceptually simpler (relies on reversing edges) | More intricate with low-link values |
| Practical Use | Easy to explain and implement | Often more efficient in practice |
Applications of Strongly Connected Components
- Program Analysis: SCCs help in detecting cycles and optimizing dependency resolution in compilers.
- Social Network Analysis: Clusters of users who are mutually connected through follow/like relationships can be identified using SCCs.
- Deadlock Detection: In operating systems and distributed systems, SCCs help in analyzing circular wait conditions.
- Electronic Circuit Design: SCCs reveal potential feedback loops in circuit analysis.
Conclusion
Strongly Connected Components are fundamental to understanding the structure of directed graphs. Both Kosaraju’s and Tarjan’s Algorithms solve the SCC problem in linear time, albeit with different approaches. While Kosaraju uses two DFS passes with a transpose graph, Tarjan’s method leverages low-link values and a single DFS traversal. Together, they provide essential tools for solving complex graph problems in real-world applications.