String Compression: Run-Length and Other Techniques Explained with Examples

String compression is a fundamental concept in computer science, widely used in data storage, efficient transmission, and optimizing performance. At its core, string compression reduces the size of data by removing redundancies while still allowing the original to be reconstructed. One of the simplest forms of string compression is Run-Length Encoding (RLE), along with advanced techniques such as Huffman Coding and dictionary-based methods.

Table of Contents

Why String Compression Matters

Large amounts of textual and binary data require efficient storage and fast transmission. Compression helps to:

Reduce memory usage
Optimize file storage and disk space
Improve network transfer speeds
Enable efficient algorithmic operations

Run-Length Encoding (RLE)

Run-Length Encoding compresses strings by replacing consecutive repeated characters with a single instance of the character followed by the count of repetitions. It works best on data with many repeating patterns (such as images with uniform color or spaces in text).

Example of RLE

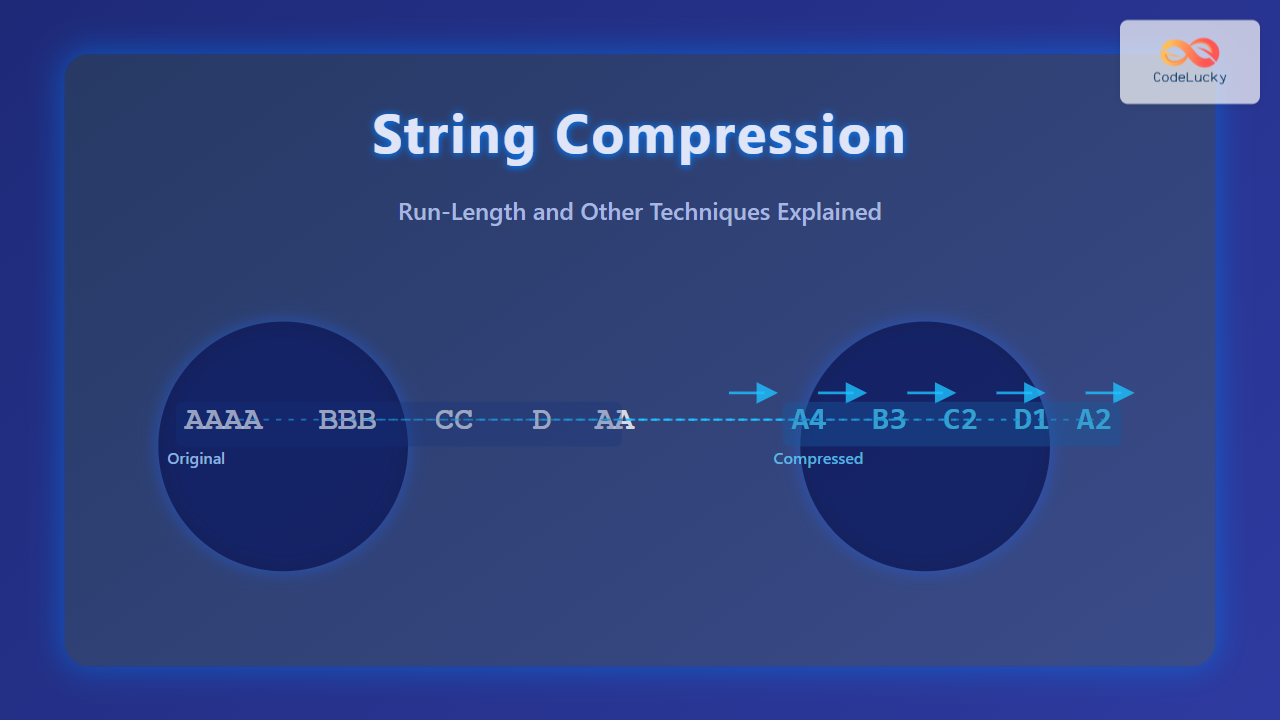
Original String:  AAAABBBCCDAA
Compressed Form: A4B3C2D1A2

Here, instead of storing repeated sequences explicitly, we store character-count pairs. While RLE significantly reduces size for repetitive data, it may even increase size if the input lacks repetitions (e.g., “ABC” → “A1B1C1”).

Python Implementation of RLE


def run_length_encode(s: str) -> str:
    if not s:
        return ""
    encoded = []
    count = 1
    for i in range(1, len(s)):
        if s[i] == s[i-1]:
            count += 1
        else:
            encoded.append(s[i-1] + str(count))
            count = 1
    encoded.append(s[-1] + str(count))
    return "".join(encoded)

print(run_length_encode("AAAABBBCCDAA"))  # Output: A4B3C2D1A2

RLE Decoding in Python


def run_length_decode(s: str) -> str:
    decoded = []
    i = 0
    while i < len(s):
        char = s[i]
        j = i + 1
        count = ""
        while j < len(s) and s[j].isdigit():
            count += s[j]
            j += 1
        decoded.append(char * int(count))
        i = j
    return "".join(decoded)

print(run_length_decode("A4B3C2D1A2"))  # Output: AAAABBBCCDAA

Other String Compression Techniques

While RLE is simple, it is not universally effective. More sophisticated techniques provide better compression rates:

1. Huffman Coding

Huffman Coding is an entropy-based technique that assigns shorter binary codes to frequent characters and longer codes to rare ones. It produces a variable-length prefix code, ensuring no code is a prefix of another.

2. Dictionary-Based (Lempel-Ziv)

Dictionary-based compression techniques, like LZW (Lempel–Ziv–Welch), build a dictionary of substrings encountered and replace repeating patterns with dictionary references. These techniques are widely used in formats like GIF, PNG, and ZIP files.

3. Burrows-Wheeler Transform (BWT)

The Burrows-Wheeler Transform is a block-sorting algorithm that rearranges a string into a form particularly suited for run-length and entropy-based compression techniques. It is the backbone of modern compression algorithms like bzip2.

Comparing Compression Techniques

Technique	Best For	Compression Ratio	Complexity
Run-Length Encoding	Highly repetitive data	Low to High	O(n)
Huffman Coding	General textual data	Medium	O(n log n)
LZW / Dictionary Based	Files with repeated substrings (e.g., images, text)	High	O(n)
Burrows-Wheeler + Huffman	Block data compression	Very High	O(n log n)

Interactive Visualization

Let’s try a step-by-step breakdown of how RLE works:


Step 1: Input = "AAAABBBCCDAA"
Step 2: Group consecutive symbols → [AAAA], [BBB], [CC], [D], [AA]
Step 3: Count each → A4, B3, C2, D1, A2
Step 4: Output = "A4B3C2D1A2"

Applications of String Compression

String compression has real-world use cases such as:

File Storage: Reducing text and image size improves disk efficiency.
Data Transmission: Speeds up network transfer.
Databases: Compressed storage improves query performance.
Search Engines: Store large indexes in compressed formats for faster lookups.

Conclusion

String compression techniques, from simple Run-Length Encoding to advanced algorithms like Huffman Coding and LZW, are at the heart of modern computing. Choosing the right algorithm depends on the nature of the data and the expected compression ratio. While RLE is excellent for repeated patterns, entropy- and dictionary-based compression excel for diverse text and multimedia data. A solid understanding of these methods enables developers to optimize storage, transmission, and computational efficiency.