When working with spatial data like points in 2D or 3D space, simple arrays and lists often become inefficient for processing queries such as nearest-neighbor search, collision detection, or spatial indexing. This is where spatial data structures like quadtrees and KD-Trees come into play. Widely applied in computer graphics, GIS systems, pathfinding, and machine learning, these data structures optimize searching within multidimensional spaces efficiently.
Introduction to Spatial Data Structures
A spatial data structure is designed to represent objects located in space, supporting fast queries like:
- Finding all points within a rectangular or circular range
- Locating the nearest neighbor to a given point
- Efficiently detecting collisions in 2D/3D environments
Among the many spatial structures, quadtrees and KD-Trees are the most popular. Let’s explore each in detail.
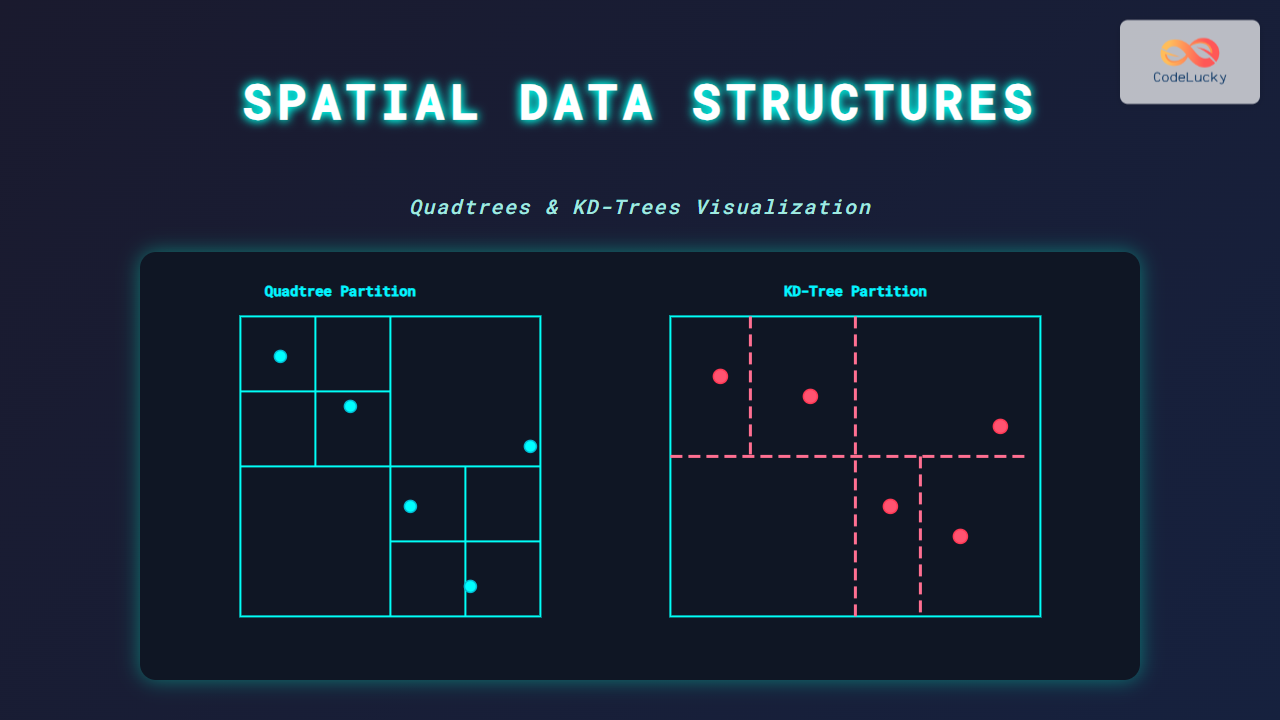
Quadtrees Explained
A quadtree recursively subdivides a 2D plane into four quadrants (top-left, top-right, bottom-left, bottom-right). Each node represents a region of space, and subdivision continues until each cell reaches a minimal size or contains below a threshold of objects.
This structure is especially useful in:
- Game development: efficiently determining nearby objects in a 2D map
- GIS: querying geographical boundaries
- Image processing: compressing images by subdividing homogeneous regions
Python Example: Quadtree
class Quadtree:
def __init__(self, boundary, capacity):
self.boundary = boundary # [x, y, width, height]
self.capacity = capacity # max points before subdivision
self.points = []
self.divided = False
def subdivide(self):
x, y, w, h = self.boundary
hw, hh = w/2, h/2
self.nw = Quadtree([x, y, hw, hh], self.capacity)
self.ne = Quadtree([x+hw, y, hw, hh], self.capacity)
self.sw = Quadtree([x, y+hh, hw, hh], self.capacity)
self.se = Quadtree([x+hw, y+hh, hw, hh], self.capacity)
self.divided = True
def insert(self, point):
x, y = point
bx, by, w, h = self.boundary
if not (bx <= x < bx+w and by <= y < by+h):
return False
if len(self.points) < self.capacity:
self.points.append(point)
return True
else:
if not self.divided:
self.subdivide()
return (self.nw.insert(point) or
self.ne.insert(point) or
self.sw.insert(point) or
self.se.insert(point))
This code shows how points can be inserted and subdivided automatically.
KD-Trees Explained
A KD-Tree (k-dimensional tree) is a binary tree that partitions space alternately along each dimension. For 2D points, the first split is along the x-axis, then the y-axis, and so on recursively.
KD-Trees are best suited for:
- Nearest neighbor search: quickly finding closest points
- Machine learning: used in KNN classifiers
- Range queries: efficiently filtering points in multidimensional rectangles
Python Example: KD-Tree
class KDNode:
def __init__(self, point, axis, left=None, right=None):
self.point = point
self.axis = axis
self.left = left
self.right = right
def build_kdtree(points, depth=0):
if not points:
return None
k = len(points[0]) # dimensions
axis = depth % k
points.sort(key=lambda p: p[axis])
median = len(points) // 2
return KDNode(
points[median],
axis,
build_kdtree(points[:median], depth+1),
build_kdtree(points[median+1:], depth+1)
)
The KD-Tree alternates splitting axis based on depth, creating a balanced partition of the space.
Visual Example: KD-Tree Partitioning
Comparing Quadtrees and KD-Trees
| Feature | Quadtree | KD-Tree |
|---|---|---|
| Type of Partition | Divides space into four quadrants | Binary split along alternating axes |
| Best For | 2D spatial indexing, graphics | Nearest-neighbor search, multidimensional queries |
| Complexity | O(log n) average search | O(log n) average, but degrades with skewed data |
| Applications | Games, GIS, Image Processing | Machine Learning, Range Searching |
Interactive Visualization
To better understand these structures, one can create an interactive Quadtree or KD-Tree visualization in Python using matplotlib or web-based JavaScript libraries like d3.js. Example idea:
- Display a 2D scatterplot of points.
- Show splitting lines for KD-Tree or quadrants for Quadtree.
- Allow inserting points dynamically to visualize subdivisions.
Conclusion
Both Quadtrees and KD-Trees are essential spatial data structures in computational geometry. Quadtrees excel in uniform 2D partitioning, while KD-Trees shine in multidimensional nearest-neighbor searches. Choosing the right structure depends on the application domain—be it real-time rendering in games, geographical systems, machine learning classifiers, or scientific simulations.
Mastering these data structures will help you solve complex spatial problems efficiently, making your algorithms more scalable and your applications faster.