Simulated Annealing is a versatile and powerful probabilistic optimization technique inspired by the physical process of annealing in metallurgy. It is especially useful for solving complex optimization problems where traditional algorithms may get stuck in local optima. This article delves deep into the concept, working principle, algorithmic steps, and practical examples of simulated annealing with visual and interactive explanations suitable for learners, researchers, and practitioners alike.
Understanding Simulated Annealing
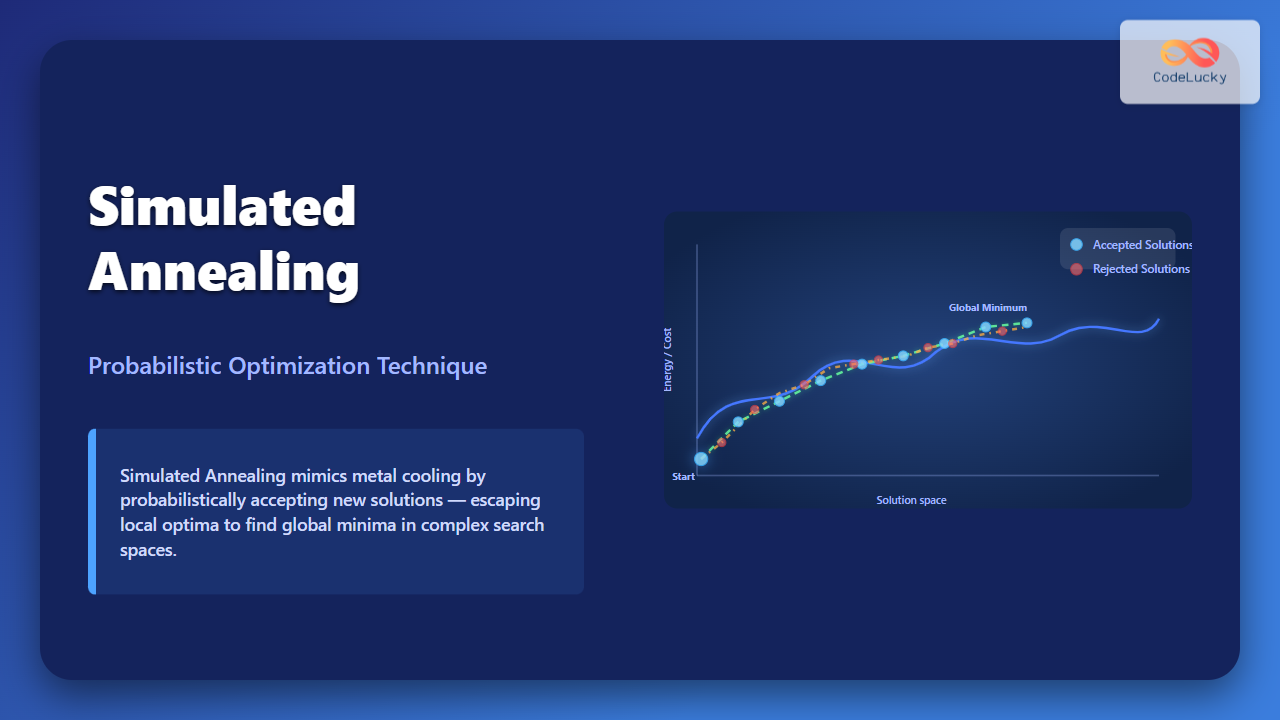
Simulated Annealing (SA) is a metaheuristic inspired by the way metals cool and crystallize. During metal annealing, heat is gradually decreased allowing atoms to settle into a low-energy, stable configuration—essentially optimizing their arrangement. SA applies the same principle to optimization problems by exploring the solution space probabilistically, allowing occasional acceptance of worse solutions to escape local optima and eventually converging to a globally optimal or near-optimal solution.
Key Concepts and Terminology
- State or Solution: A candidate solution in the search space.
- Energy or Cost Function: A metric that quantifies solution quality (lower is better).
- Temperature (T): Controls the acceptance of worse solutions; starts high and cools down.
- Cooling Schedule: A strategy to reduce temperature gradually over iterations.
- Neighbor Solution: A solution close to the current one, generated by a small random change.
Simulated Annealing Algorithm Explained
The simulated annealing algorithm iteratively explores solutions by probabilistically deciding between accepting improvements, or with some probability, accepting worse solutions to avoid premature convergence:
1. Initialize current solution S and set initial temperature T
2. Repeat while T > minimum threshold
a. Generate a neighbor solution S_new from S
b. Calculate the energy difference ΔE = E(S_new) - E(S)
c. If ΔE < 0:
- Accept S_new as current solution (better solution)
d. Else:
- Accept S_new with probability P = exp(-ΔE / T)
e. Decrease temperature T according to cooling schedule
3. Return the best solution found
Example: Minimizing a Cost Function
Consider the task of minimizing the mathematical function \( f(x) = x^2 + 10 \sin(x) \) over the interval \(-10 \leq x \leq 10\), which has many local minima.
The simulated annealing approach helps escape local valleys and find the global minimum by allowing uphill moves early on.
Visualizing Simulated Annealing Progress
When to Use Simulated Annealing?
Simulated annealing is best suited for:
- Complex optimization problems with many local optima
- Combinatorial problems like the Traveling Salesman Problem, job scheduling, and layout optimization
- Problems where gradient information is unavailable or unreliable
- Situations where a good approximate solution is acceptable within reasonable time
Advantages and Limitations
| Advantages | Limitations |
|---|---|
| Can escape local optima due to probabilistic uphill moves | Slow convergence, requires careful cooling schedule tuning |
| Simple implementation and widely applicable | Parameter sensitivity: initial temperature, cooling rate affect results |
| Works without gradient information | Not guaranteed to find true global optimum |
Mermaid Diagram: Cooling Schedules
Summary
Simulated Annealing is a probabilistic optimization strategy that cleverly mimics physical annealing to find near-optimal solutions in difficult search spaces. By permitting non-improving moves at controlled probabilities, it overcomes the limitations of greedy algorithms plagued by local optima. With careful parameter tuning and proper cooling schedules, SA remains a valuable method for a broad class of optimization problems.