Set Cover Problem: Greedy Approximation Algorithm Explained with Examples

The Set Cover Problem is a foundational combinatorial optimization challenge that frequently appears in computer algorithms, operations research, and theoretical computer science. It is a classic NP-hard problem, meaning finding an exact minimal set cover quickly is infeasible for large inputs. This article deeply explores the Greedy Approximation Algorithm to solve the Set Cover Problem, providing step-by-step explanations, real-world examples, and intuitive visualizations.

Table of Contents

What is the Set Cover Problem?

The problem can be stated as follows: Given a universal set U and a collection of subsets S = {S1, S2, ..., Sn} whose union equals U, the goal is to find the smallest number of subsets in S that together cover all elements in U.

Formally:

Universal set U = {e1, e2, ..., em}
Collection of subsets S = {S1, S2, ..., Sn}, each Si ⊆ U
Find minimum C ⊆ S such that ⋃(Si ∈ C) Si = U.

Why Set Cover Problem is Hard?

The Set Cover Problem is NP-complete, which means there is no known polynomial-time algorithm to solve it optimally for all general cases. For large datasets, exhaustive search is computationally prohibitive because it involves checking all combinations of subsets.

Because of its significance in practical applications such as sensor placement, resource allocation, and network design, efficient approximate solutions are crucial. The Greedy Approximation Algorithm is the most widely studied heuristic because it is simple, fast, and provides a guaranteed approximation ratio.

Greedy Approximation Algorithm for Set Cover

The Greedy Algorithm iteratively selects the subset that covers the largest number of uncovered elements until all elements in U are covered.

Algorithm Steps:

Initialize the cover set C = ∅ and uncovered elements as U.
Select the subset S_i in S that covers the maximum number of uncovered elements.
Add S_i to C, mark its elements as covered.
Repeat steps 2-3 until all elements in U are covered.
Return C as the approximate set cover.

Approximation Quality

The greedy approach finds a cover whose size is at most H(d) times the size of an optimal cover, where d is the size of the largest subset and H(d) is the Harmonic number approximately equal to ln(d) + 1. This makes the greedy algorithm an O(log n) approximate algorithm.

Example with Visual Explanation

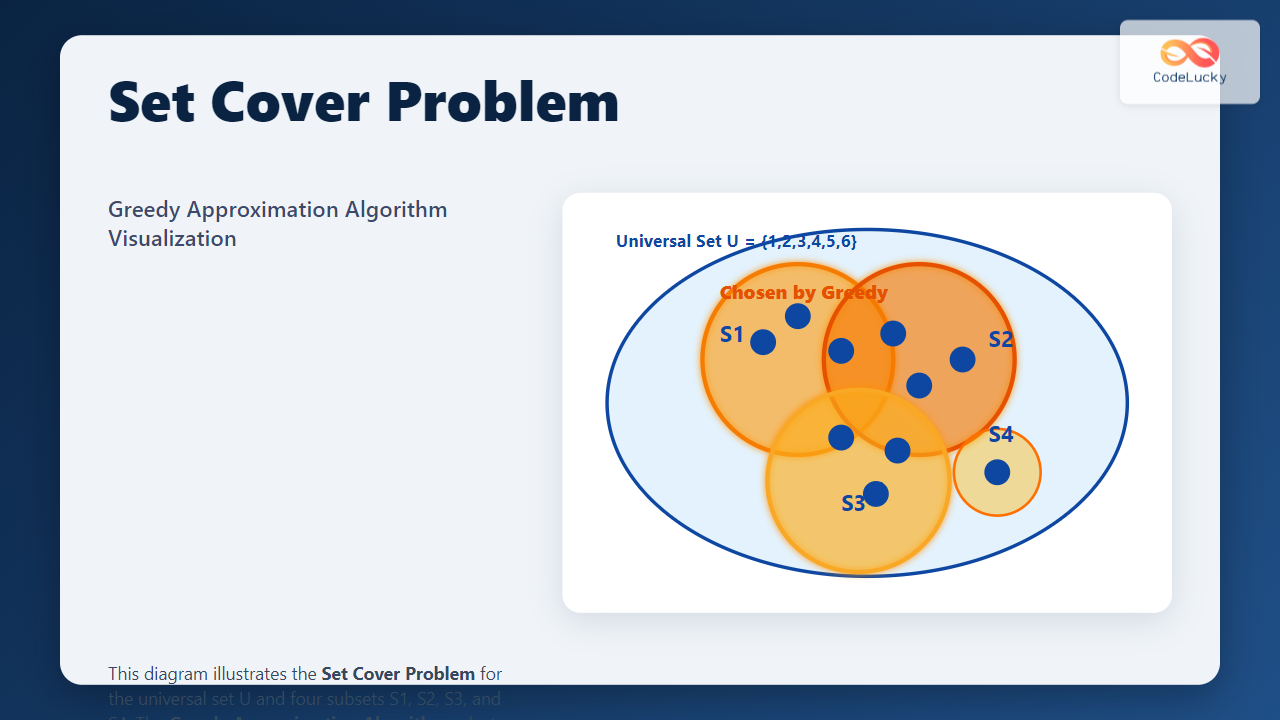
Consider the universal set U = {1, 2, 3, 4, 5, 6} and subsets:

S1 = {1, 2, 3}
S2 = {2, 4, 5}
S3 = {3, 5, 6}
S4 = {6}

We want to cover all elements in U with minimum subsets.

Step 1: Start with all uncovered elements {1,2,3,4,5,6}. The subset covering the most elements is S1 (3 elements). Select S1.

Step 2: Covered elements: {1,2,3}, remaining uncovered: {4,5,6}. Now choose subset covering most uncovered elements:

S2 covers {4,5} (2 elements)
S3 covers {5,6} (2 elements)
S4 covers {6} (1 element)

Choose either S2 or S3. Select S2.

Step 3: Covered elements: {1,2,3,4,5}, uncovered: {6}. The only subset covering 6 is S3 or S4. Choose S3 because it covers 2 elements but only one uncovered remains anyway.

Result: The greedy cover is {S1, S2, S3}.

Interactive Visualization (Concept)

For a dynamic learning experience, interactive tools can allow users to select subsets and see coverage progress in real-time. Unfortunately, this static article format cannot embed interactive elements. However, visual tools like the diagrams above provide clear intuition on the algorithm’s workflow.

Summary and Uses

The Greedy Approximation Algorithm is a practical and efficient heuristic for the Set Cover Problem, especially suited for large-scale data where exact algorithms are infeasible. Though it may not always find the minimal cover, its logarithmic approximation guarantee makes it a powerful tool in fields like:

Network design and monitoring
Resource allocation
Data mining and machine learning feature selection
Facility location planning

Understanding and implementing this algorithm is essential for algorithm designers and computer scientists tackling real-world combinatorial coverage challenges.