The Secretary Problem, also known as the Marriage Problem or Optimal Stopping Problem, is a classical problem in Optimal Stopping Theory, which focuses on devising a strategy to maximize the probability of selecting the best option from a sequence of rankable candidates appearing sequentially. This problem elegantly blends probability, decision theory, and algorithms to answer how one should stop examining candidates to pick the very best, given that decisions are irrevocable.
What is the Secretary Problem?
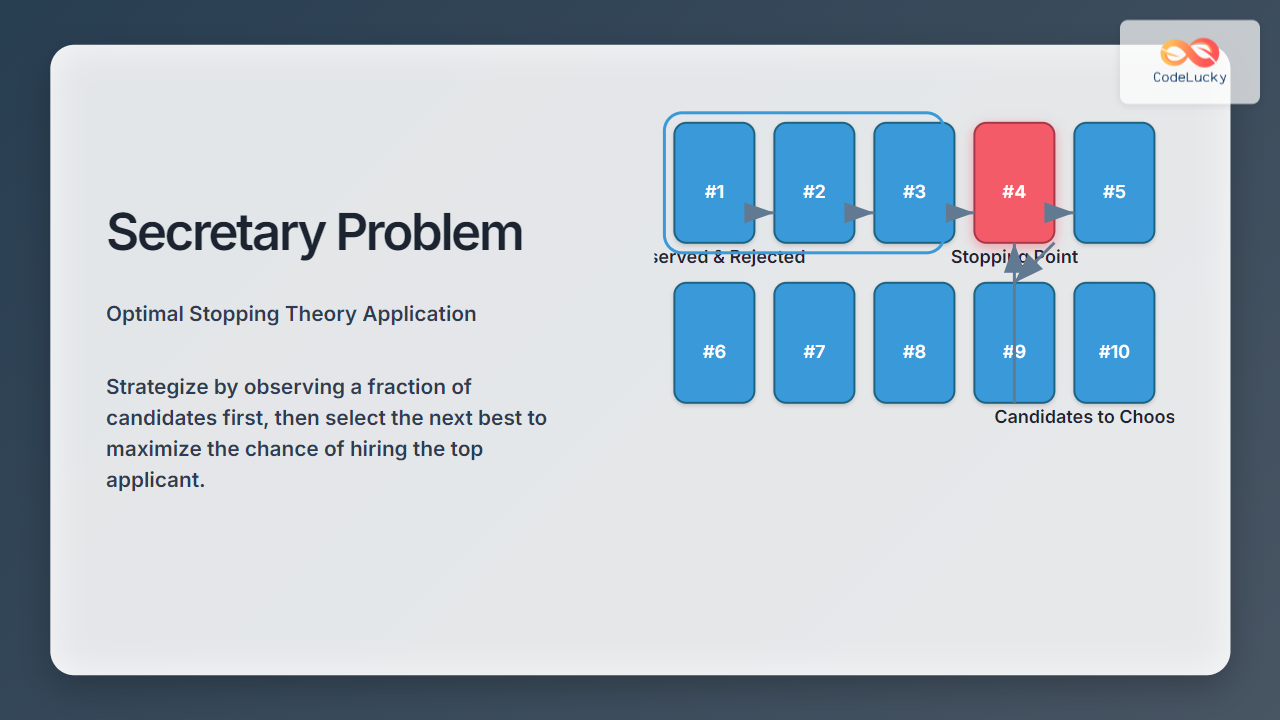
Imagine interviewing n applicants for a secretarial position, where applicants are interviewed one by one in random order. After each interview, the decision maker must either hire that candidate immediately or reject them forever and continue the interview process with no turning back. The goal: select the single best candidate out of all n.
The catch is that the candidates can only be compared relative to those already interviewed—not by absolute rank—making the problem tricky and rich for mathematical exploration.
Formal Definition
Let there be n candidates arriving in random order. After interviewing the k-th candidate:
- You can either choose that candidate, ending the process, or
- Reject that candidate, continuing with the next.
The objective is to maximize the probability of selecting the overall best candidate.
Key Insight: The “37% Rule”
Optimal stopping theory proves the best way to maximize the chance of selecting the best candidate is to first reject approximately the first 37% of candidates — using this initial batch only to gather information about candidate quality — then hire the next candidate who is better than all previously seen.
Mathematically, the stopping threshold \( r \) is:
r ≈ n / e ≈ 0.37n
Where \( e \) is Euler’s number (~2.718).
Why Does the 37% Rule Work?
By rejecting the first 37%, you gather a strong sample to benchmark future candidates. While rejecting those first, you do not miss the chance of a better candidate afterward because the sampled best is a realistic standard. This balances letting through too many early (low-rank) candidates or risking passing the best early candidate.
Step-by-Step Example
Suppose there are 10 candidates (n=10). The stopping rule suggests rejecting the first 3 or 4 candidates (as \( 10 / e \approx 3.68 \)).
- Interview candidates 1 through 4 without hiring, just observe and note the rank of the best so far.
- From candidate 5 onwards, hire the first candidate who is better than all previously interviewed.
- If no one superior appears, hire the last candidate by default.
Example sequence (ranks from best=1 to worst=10): 6, 10, 3, 8, 4, 1, 9, 5, 7, 2
- First 4 candidates observed: best is 3 (candidate 3)
- Next candidates evaluated:
- Candidate 5: rank 4 (not better than 3)
- Candidate 6: rank 1 (better than 3), so hire candidate 6 immediately.
Implementing in Code (Python Example)
import random
def secretary_problem(candidates):
n = len(candidates)
r = int(n / 2.718) # approximately 37%
# Observe first r candidates and find the best rank among them
best_so_far = max(candidates[:r])
# Pick the first candidate better than the observed best
for i in range(r, n):
if candidates[i] > best_so_far:
return i, candidates[i]
# If no candidate better, pick last candidate
return n-1, candidates[-1]
# Random ranks simulation, higher means better
candidates = random.sample(range(1, 101), 10)
picked_index, picked_value = secretary_problem(candidates)
print("Candidates (rank order):", candidates)
print("Picked candidate index:", picked_index)
print("Picked candidate rank:", picked_value)
Visualizing Decision Process
Probability of Success
The exact probability of successfully selecting the best candidate when following the optimal stopping rule approaches about 37% as \( n \rightarrow \infty \). This counterintuitive result shows that even with optimal strategy, there’s about a one-in-three chance of success due to the inherent uncertainty.
Extensions and Variations
- With recall allowed: The problem changes when you can recall earlier candidates.
- Multiple best candidates: Selecting among the top k candidates instead of strictly the best.
- Unknown number of candidates: Variants exist when total candidate numbers are not known beforehand.
Summary
The Secretary Problem demonstrates the power of Optimal Stopping Theory through an elegant, practical scenario. The “37% rule” provides a simple yet mathematically justified guideline for real-world decisions where timing and imperfect information challenge optimal choices.