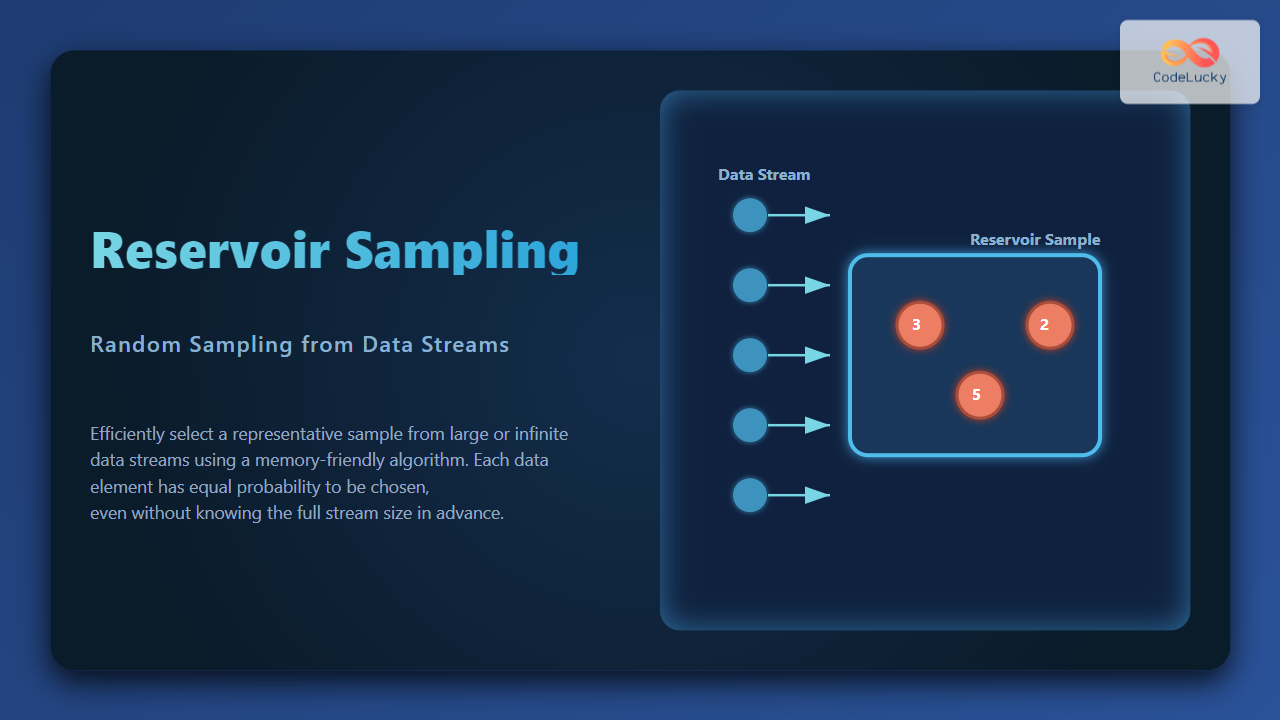
Reservoir Sampling: Random Sampling from Data Streams Explained with Examples

When dealing with very large datasets or infinite data streams, storing all the data in memory and then performing a random sample is nearly impossible. The solution to this problem is Reservoir Sampling, a clever random sampling algorithm that allows us to select exactly k random elements from a stream of n items, without knowing n in advance and without storing the entire dataset.

In this article, we will explore Reservoir Sampling step by step, with detailed examples, diagrams, and working code to fully understand how this algorithm works and why it is essential in modern data processing, machine learning, and big data applications.

Table of Contents

What is Reservoir Sampling?

Reservoir Sampling is an algorithm that allows us to maintain a representative sample of size k from a data stream of unknown or very large size. It guarantees that each item has an equal probability of being included in the final reservoir sample.

Formally, given a stream of n items and a reservoir size k:

When the first k items arrive, put them directly into the reservoir.
For every item at index i (where i > k), replace a randomly chosen element from the reservoir with probability k / i.
This ensures every element in the stream has an equal chance of being part of the reservoir.

Why is Reservoir Sampling Important?

Reservoir Sampling is used in scenarios where data is too large or too fast to store in full, such as:

Social media platforms analyzing billions of posts or user interactions.
Database systems processing live transactions in real time.
Machine learning pipelines needing unbiased representation of continuously streaming data.
Network traffic monitoring where storing all packets is infeasible.

How Reservoir Sampling Works

To understand the Reservoir Sampling algorithm in action, let’s walk through each step with a small example.

Example Walkthrough

Suppose we want to sample k = 3 items from a stream of numbers [10, 20, 30, 40, 50].

First 3 items [10, 20, 30] are directly placed into the reservoir.
Next item (40) has probability 3/4 of being selected to replace an element in the reservoir.
Next item (50) has probability 3/5 of being selected.
At the end, the reservoir contains a random sample of 3 items with equal probability.

Python Implementation of Reservoir Sampling


import random

def reservoir_sampling(stream, k):
    reservoir = []
    
    # Fill the reservoir with first k items
    for i in range(k):
        reservoir.append(stream[i])
    
    # Process the rest of the stream
    for i in range(k, len(stream)):
        j = random.randint(0, i)
        if j < k:
            reservoir[j] = stream[i]
    
    return reservoir

# Example usage
data_stream = [10, 20, 30, 40, 50, 60, 70]
sample = reservoir_sampling(data_stream, 3)
print("Random Sample:", sample)

Running this function multiple times will produce different sets of samples, but each element in the stream will have the same chance of ending up in the final sample.

Step-by-Step Example with Visual Output

Let’s run through a concrete example where k = 2 and the data stream is [A, B, C, D, E].

At the end, the reservoir contains 2 randomly chosen items from the stream, each equally likely.

Probability Proof (Why it Works)

The algorithm guarantees fairness. Let’s say the current element is at position i. The probability of it being chosen is:

Probability of being inserted into reservoir at step i = k / i.
Probability of not being replaced in the later steps = product of (1 – k/j) for j > i.
Final probability simplifies to exactly k / n for each item.

Applications of Reservoir Sampling

Streaming analytics in platforms like Apache Kafka, Spark Streaming.
Data pre-processing for machine learning on continuous training data.
Randomized algorithms where uniform randomness is required.
Optimizing bandwidth and computing resources in large distributed systems.

Interactive Demo (Python)


import random

def interactive_demo(stream, k):
    reservoir = []
    print("Initial Stream:", stream)
    
    # Fill initial reservoir
    for i in range(k):
        reservoir.append(stream[i])
    print("Step 1 - Initial reservoir:", reservoir)
    
    # Replace with probabilities
    for i in range(k, len(stream)):
        j = random.randint(0, i)
        if j < k:
            replaced = reservoir[j]
            reservoir[j] = stream[i]
            print(f"Step {i+1}: Replaced {replaced} with {stream[i]}, Reservoir: {reservoir}")
        else:
            print(f"Step {i+1}: Kept reservoir unchanged: {reservoir}")
    return reservoir

interactive_demo([1,2,3,4,5,6], 2)

Conclusion

Reservoir Sampling is a simple yet powerful algorithm for random sampling from large or infinite streams. It provides uniform probability, efficient memory usage, and constant-time processing per item. Because of these advantages, it is widely used in big data, databases, and online machine learning systems.

When you need a fair random subset from an otherwise overwhelming data stream, Reservoir Sampling is the go-to algorithm to keep your reservoir unbiased and representative.