Randomized Rounding: Converting Linear Programming Solutions to Integral Solutions

Randomized rounding is a powerful technique in computer science and optimization that converts fractional solutions produced by linear programming (LP) relaxations into integral solutions. This approach is widely used in approximation algorithms where exact combinatorial optimization problems are hard to solve directly.

In this article, we will explore the concept of randomized rounding in detail, explain its significance in converting fractional LP solutions to integral ones, and illustrate with examples and visualizations for clarity. Interactive explanation and mermaid diagrams will help deepen understanding.

Table of Contents

What Is Randomized Rounding?

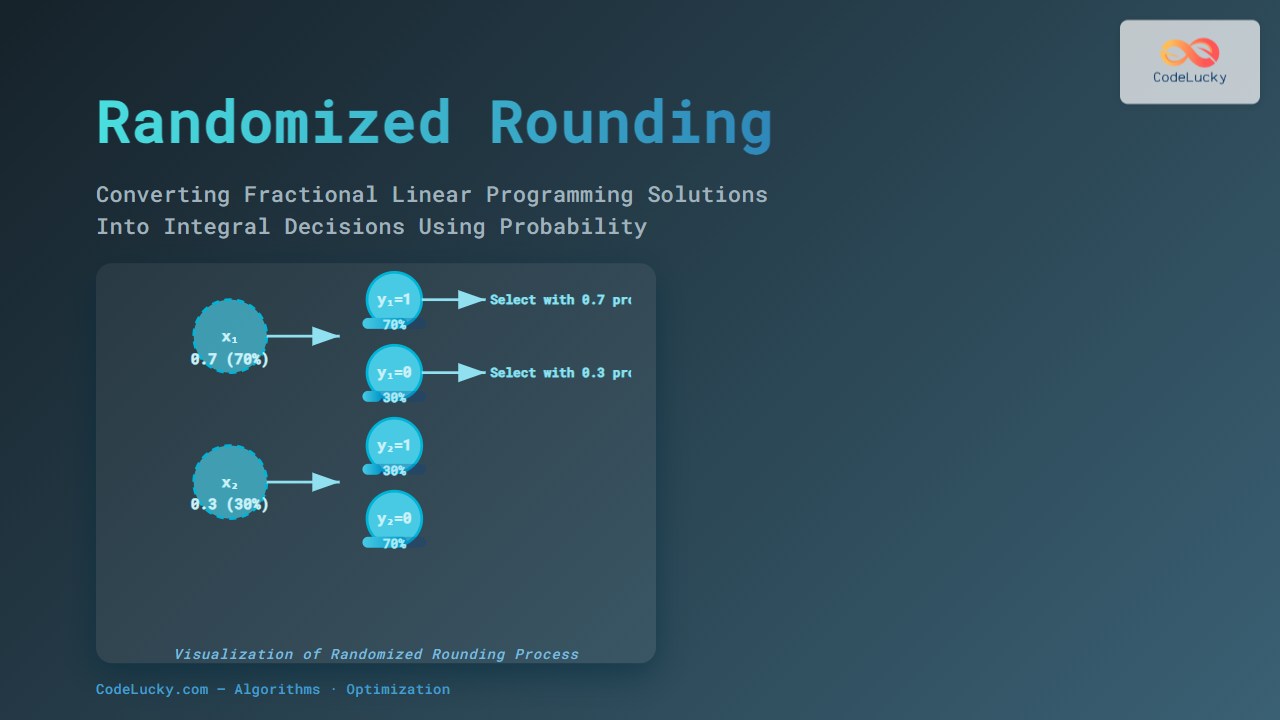
Randomized rounding is a probabilistic technique that converts fractional solutions of an LP problem into discrete or integral solutions. The LP relaxation often gives values between 0 and 1, which cannot be used directly in scenarios such as selecting items (0 or 1), assigning jobs, or picking sets.

Instead of simply rounding deterministically, randomized rounding treats the fractional value as a probability to decide the final integral value. For example, if a variable’s value in the LP solution is 0.7, it is rounded up to 1 with 70% chance and to 0 with 30% chance.

Why Randomized Rounding?

Maintains Expected Value: The expected value of the rounded solution remains the same as the fractional LP solution.
Simple & Efficient: It is easy to implement and fast for large-scale problems.
Approximation Guarantees: It helps derive approximation bounds for hard combinatorial problems.

How Randomized Rounding Works: Step-by-Step

Formulate the LP Relaxation: Replace integer constraints with continuous ones, usually between 0 and 1.
Solve the LP: Obtain an optimal fractional solution vector \( \mathbf{x} = (x_1, x_2, \ldots, x_n) \) where each \( x_i \in [0,1] \).
Randomized Rounding: For each \( x_i \), generate a random number \( r \in [0,1] \). If \( r \leq x_i \), then set the integral solution \( y_i = 1 \), else \( y_i = 0 \).
Output the Integral Solution: The \( \mathbf{y} = (y_1, \ldots, y_n) \) is an integral vector.

Example: Randomized Rounding for Set Cover Problem

Consider the Set Cover problem, where we want to select a minimum number of sets that cover all elements in a universe. LP relaxation gives fractional variables \( x_i \) representing selection probabilities.

For a LP solution like \( x = (0.6, 0.3, 0.8) \):

Set 1 is selected with 60% probability.
Set 2 is selected with 30% probability.
Set 3 is selected with 80% probability.

Applying randomized rounding means flipping a probabilistic coin for each set based on these numbers.

Code Example (JavaScript):

function randomizedRounding(lpSolution) {
  return lpSolution.map(prob => Math.random() <= prob ? 1 : 0);
}

// Sample LP fractional solution
const lpSolution = [0.6, 0.3, 0.8];
const integralSolution = randomizedRounding(lpSolution);
console.log(integralSolution);

This code outputs an integral vector each run with expected values matching the fractional solution.

Analyzing the Randomized Rounding Output

The key points in analysis are:

Expected Value: \( E[y_i] = x_i \), meaning the rounded solution’s expectation matches the LP fractional solution.
Concentration Bounds: Using Chernoff or Hoeffding bounds, the solution’s feasibility can be bounded probabilistically.
Approximation Ratios: Expected approximation quality can be demonstrated compared to the fractional optimal.

Visualizing Probability and Integral Conversion

Practical Considerations & Limitations

Randomized rounding is simple and effective, but some issues include:

Constraint Violations: Sometimes the integral solution violates constraints, which may require repeated trials or sophisticated techniques such as alteration or derandomization.
Variance: Problem-specific tweaking may be needed to control rounding variance.

Summary

Randomized rounding bridges the gap between continuous linear programming solutions and discrete integral requirements, enabling efficient approximation algorithms. By interpreting fractional values as probabilities to determine their integral counterparts, this method offers simple implementation and strong theoretical grounding in approximation guarantees.

For deeper study, consider how derandomization techniques or altered rounding methods help enforce constraints strictly while keeping close to the expected performance.