Hash tables are one of the most widely used data structures in computer science because they provide average case O(1) search, insert, and delete operations. However, an inevitable issue in hashing is collisions — when two different keys map to the same index. Quadratic Probing is a popular collision resolution technique used to minimize clustering in hash tables, improving access speed and efficiency.
What is Quadratic Probing?
Quadratic Probing is an open addressing method for resolving hash collisions. Instead of linearly probing the next slot (like Linear Probing), it uses a quadratic function of the form:
index = (hash(key) + c1 * i + c2 * i²) % m
- hash(key) → Original hash function result
- i → Probe number (0, 1, 2, …)
- c1 and c2 → Constants that control the step size
- m → Size of the hash table
This quadratic term ensures that consecutive probes jump further apart, reducing primary clustering that occurs in Linear Probing.
Why Use Quadratic Probing?
Quadratic probing addresses two major concerns in collision resolution:
- Reduces Primary Clustering: Keys forming a dense cluster in linear probing are spread apart in quadratic probing.
- Maintains Locality: Unlike double hashing, quadratic probing still explores nearby slots, ensuring better cache performance.
How Quadratic Probing Works (Step-by-Step Example)
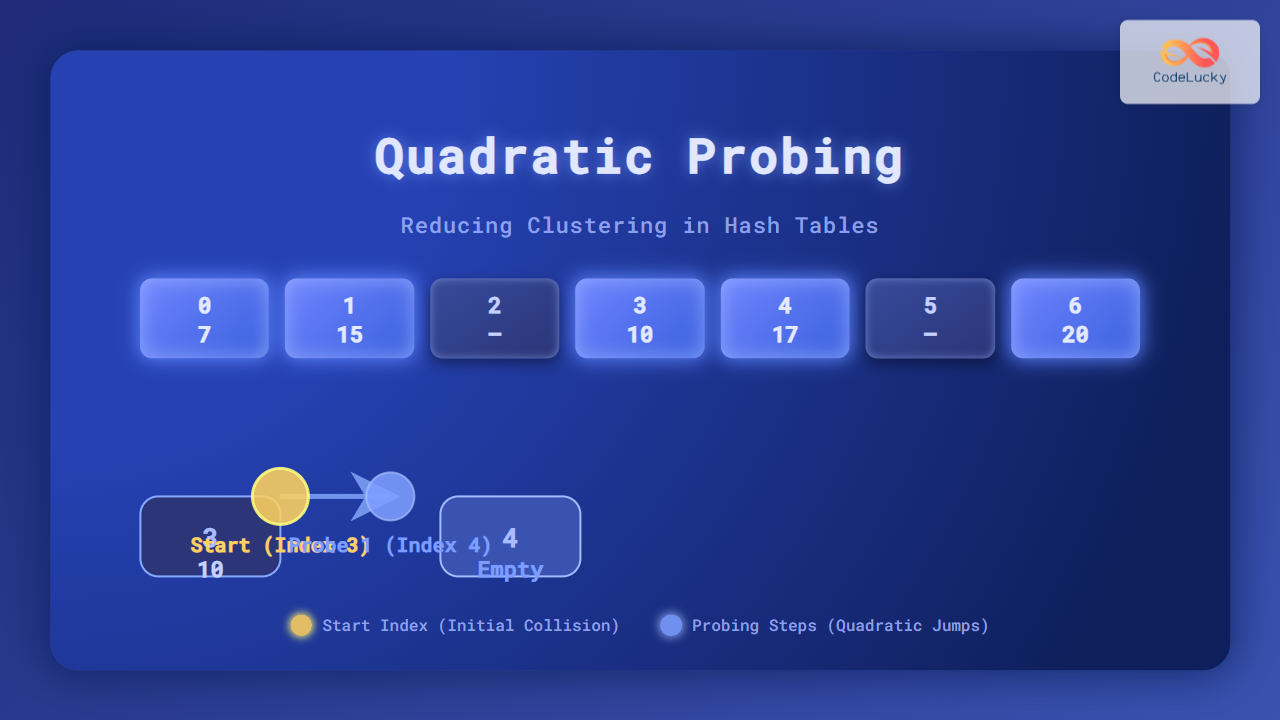
Let’s take a hash table of size 7 and use hash(key) = key % 7. Suppose we insert: [10, 20, 15, 7].
- Insert 10 → index = 10 % 7 = 3 (slot 3 empty → place 10)
- Insert 20 → index = 20 % 7 = 6 (slot 6 empty → place 20)
- Insert 15 → index = 15 % 7 = 1 (slot 1 empty → place 15)
- Insert 7 → index = 7 % 7 = 0 (slot 0 empty → place 7)
Now, insert 17:
- hash(17) = 17 % 7 = 3 → slot 3 occupied by 10
- Probe i=1: (3 + 1²) % 7 = 4 → empty → insert 17 at index 4
Notice how instead of clustering consecutively, Quadratic Probing spaced out the placement at index 4 for key 17.
Comparison with Other Methods
| Method | Collision Resolution | Clustering |
|---|---|---|
| Linear Probing | Sequential next slot | Prone to primary clustering |
| Quadratic Probing | Quadratic interval jumps | Reduces clustering significantly |
| Double Hashing | Probe step size from second hash | Best but more computation |
Quadratic Probing Algorithm (Pseudocode)
function insert(hashTable, key):
for i from 0 to table_size - 1:
index = (hash(key) + c1*i + c2*i*i) % table_size
if hashTable[index] is empty:
hashTable[index] = key
return
throw "Hash Table Full"
Quadratic Probing Implementation in Python
class QuadraticProbingHashTable:
def __init__(self, size):
self.size = size
self.table = [None] * size
def hash(self, key):
return key % self.size
def insert(self, key):
for i in range(self.size):
index = (self.hash(key) + i*i) % self.size
if self.table[index] is None:
self.table[index] = key
return
raise Exception("Hash Table Overflow")
def display(self):
for i in range(self.size):
print(f"Index {i}: {self.table[i]}")
# Example usage
ht = QuadraticProbingHashTable(7)
keys = [10, 20, 15, 7, 17]
for k in keys:
ht.insert(k)
ht.display()
Output
Index 0: 7
Index 1: 15
Index 2: None
Index 3: 10
Index 4: 17
Index 5: None
Index 6: 20
Visualizing Quadratic Probing Probes
Suppose we search for an available index after a collision occurs for key 17 at initial index 3:
Interactive Example with Python
You can quickly test quadratic probing with different values:
ht = QuadraticProbingHashTable(11)
keys = [11, 22, 33, 44, 55, 66, 77]
for k in keys:
ht.insert(k)
ht.display()
Try adjusting table size or keys to see how clustering reduces compared to linear probing.
Advantages of Quadratic Probing
- Reduces primary clustering compared to linear probing.
- Simple to implement, only requires arithmetic operations.
- Efficient probing sequence near the initial hash index.
Limitations of Quadratic Probing
- Still suffers from secondary clustering (keys with same initial hash).
- May not cover all slots if table size is not prime.
- Requires careful choice of c1 and c2 constants.
Conclusion
Quadratic Probing offers an effective and simple approach to minimize clustering in hash tables. By leveraging quadratic intervals for probing, it spreads out colliding keys more evenly across the table. While not perfect against all clustering types, it strikes a good balance between performance and ease of implementation. For even better distribution, double hashing may be considered, but quadratic probing remains a highly practical choice in most cases.
- What is Quadratic Probing?
- Why Use Quadratic Probing?
- How Quadratic Probing Works (Step-by-Step Example)
- Comparison with Other Methods
- Quadratic Probing Algorithm (Pseudocode)
- Quadratic Probing Implementation in Python
- Visualizing Quadratic Probing Probes
- Interactive Example with Python
- Advantages of Quadratic Probing
- Limitations of Quadratic Probing
- Conclusion