Network Flow Applications: Real-World Graph Problems and Solutions

Network flow algorithms form a foundational pillar of graph theory, providing powerful tools to solve a variety of real-world problems involving resource allocation, scheduling, routing, and optimization. This article dives deep into network flow applications, explaining crucial concepts with practical examples, interactive visuals, and easy-to-understand diagrams so readers can grasp these concepts thoroughly.

What is Network Flow?

Network flow deals with the movement of “flow” through a directed graph where edges have capacities. The goal is often to determine the maximum amount of flow from a source node to a sink node without exceeding edge capacities. The two most common problems are the Maximum Flow problem and the Minimum Cut problem, which are central to many graph applications.

Real-World Applications of Network Flow

1. Traffic and Transportation Networks

In urban planning and transportation, network flow algorithms model traffic or goods movement through road networks, where edges represent roads with maximum vehicle capacity. Maximizing flow helps optimize traffic throughput and reduce congestion.

Example: A city planner wants to maximize traffic flow from a residential area to a business district through multiple roadways. Modeling the roads as edges with capacities and intersections as nodes allows calculation of the maximum number of vehicles flowing per time unit.

2. Bipartite Matching in Job Assignments

Network flow algorithms efficiently solve bipartite graph matching problems, such as assigning jobs to machines or workers to projects, ensuring maximum job assignments without conflicts.

By constructing a flow network where source connects to workers, workers connect to possible jobs, and jobs connect to sink with edges of capacity one, the maximum flow corresponds to the maximum job assignment.

3. Image Segmentation in Computer Vision

Network flow helps in segmenting images by modeling pixels or regions as nodes and edges representing similarity or boundary costs. Minimum cut algorithms partition images into meaningful segments.

4. Circulation and Supply Chain Management

Supply chains are modeled as flow networks, managing goods flow between suppliers, warehouses, and retailers. Network flow algorithms optimize distribution and ensure demands are met without exceeding supply or transport limits.

5. Project Scheduling and Resource Allocation

Network flows model tasks dependencies and resource constraints to find optimal schedules and allocate resources efficiently.

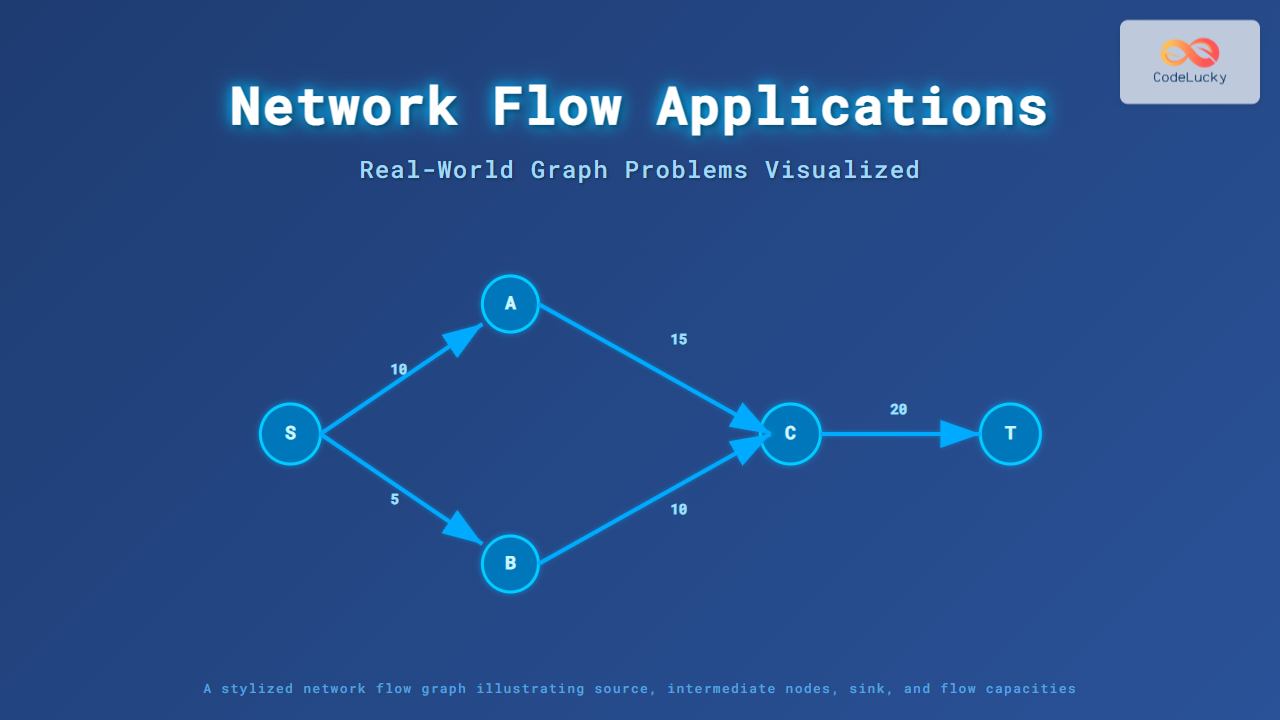
Example: Maximum Flow Calculation

Consider the following directed graph with capacities on edges:

The aim is to find the max flow from S to T. Applying the Ford-Fulkerson or Edmonds-Karp algorithm iteratively sends flow along augmenting paths until no more paths exist.

Step-by-step Example Output:

• Initial flow = 0
• Augmenting path found: S → 1 → 3 → T with flow = 7 (min capacity along path)
• Augmenting path found: S → 2 → T with flow = 4
• Augmenting path found: S → 1 → 2 → 3 → T with flow = 5
• Total max flow = 7 + 4 + 5 = 16

This output highlights how the network flow algorithm finds paths and pushes flow respecting capacities, achieving the optimal solution.

Interactive Concept: Understanding Maximum Flow

Readers are encouraged to draw their own flow networks and test augmenting paths or try interactive tools available online to simulate flow calculations. These enhance comprehension of how flow is adjusted in networks dynamically.

Summary

Network Flow algorithms are versatile tools in solving real-world problems by modeling systems as flow networks. Their applications span traffic engineering, job assignments, image segmentation, supply chains, and project scheduling. Understanding and visualizing these algorithms through examples and diagrams unlocks their potential in complex problem-solving tasks.

For developers and students aiming to master graph algorithms, integrating network flow techniques is indispensable to handle optimization and allocation challenges efficiently.