The Traveling Salesman Problem (TSP) is one of the most studied combinatorial optimization problems, central in theoretical computer science and practical applications. When the distances between points satisfy the metric property—especially Euclidean distances—a variety of strong approximation algorithms become available. This article explores the Metric TSP specifically for Euclidean distances, detailing key approximation methods, their theoretical guarantees, and practical examples with visual aids to deepen understanding.
What is Metric TSP?
The classic Traveling Salesman Problem asks: given a set of cities and pairwise distances, what is the shortest possible route that visits each city exactly once and returns to the origin? The problem is NP-hard, so finding an exact solution quickly becomes impossible for large inputs.
In Metric TSP, the distances satisfy the triangle inequality: for any three points a, b, c, the direct distance from a to c is no more than taking a detour via b (i.e., d(a,c) ≤ d(a,b) + d(b,c)).
Euclidean distances in ℝ² or ℝᵈ naturally satisfy this property, making TSP in these domains a focal point since applications in real-world routing or logistics often arise in Euclidean space.
Why Approximation?
Because the metric TSP remains NP-hard, exact methods do not scale well. Approximation algorithms offer near-optimal solutions efficiently. For metric TSP, numerous algorithms give solutions within a guaranteed factor of the optimal.
Famous results include the Christofides’ algorithm, which delivers a solution within 1.5 times the optimal cost for metric TSP, including Euclidean instances.
Christofides Algorithm: Step-by-step
The Christofides algorithm transforms the metric TSP into a structure where a feasible tour is guaranteed within 1.5 times the optimal cost. Its steps are:
- Minimum Spanning Tree (MST): Find the MST of the input graph connecting all cities with minimum total weight.
- Find Odd Degree Vertices: Identify vertices with odd degree in the MST.
- Minimum Weight Perfect Matching: Compute a minimum-weight perfect matching between these odd degree vertices.
- Combine MST and Matching: Unite edges of MST and the perfect matching, forming an Eulerian multigraph.
- Eulerian Tour to Hamiltonian Tour: Traverse the Eulerian multigraph and shortcut repeated vertices (guaranteed by triangle inequality), yielding the TSP tour.
Example: Metric TSP in Euclidean Plane
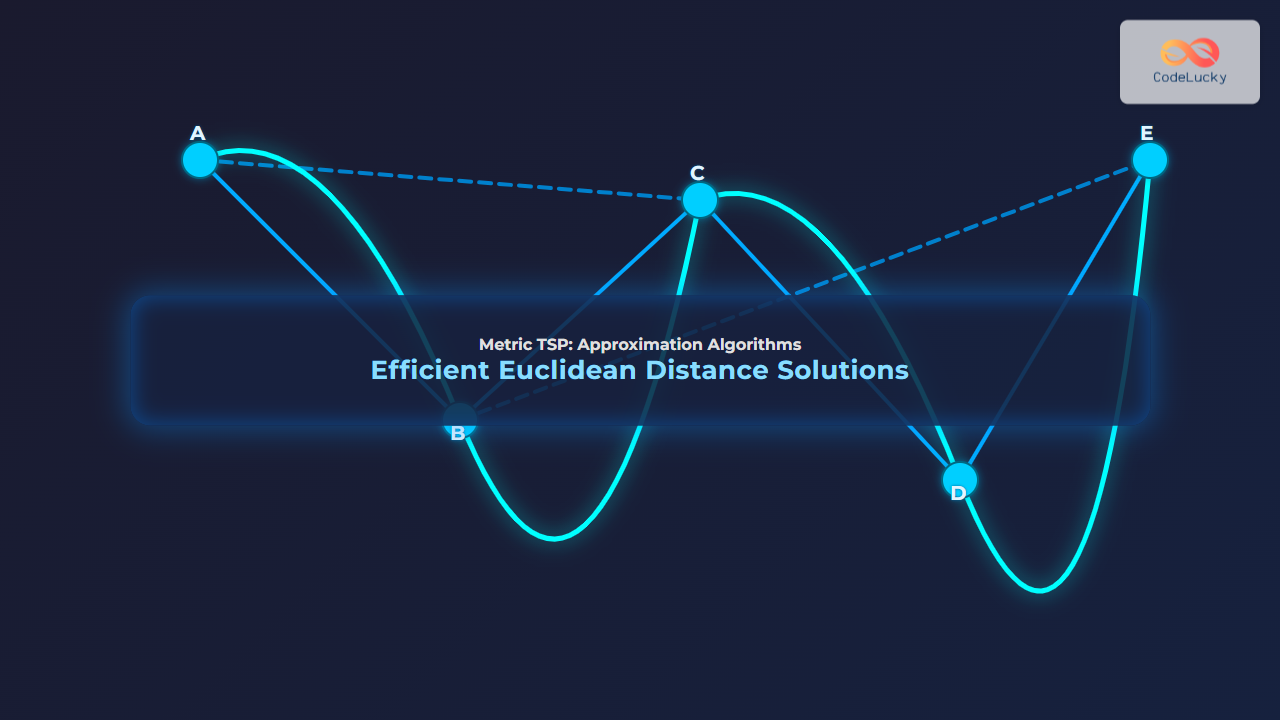
Consider five points representing cities with Euclidean distances:
A(1,2), B(4,6), C(7,3), D(10,8), E(12,1)
Constructing the MST connects these points minimizing total edge weight. Then the odd degree vertices are matched optimally, and the final path is obtained applying the Eulerian traversal and shortcut steps in Christofides algorithm.
Visualizing the MST and Matching:
Here the dotted edge between B and C indicates a perfect matching added to correct odd degrees. The final Eulerian path visits all nodes with shortcuts implemented.
Why Triangle Inequality Matters for Approximation
Without the triangle inequality, shortcutting visited vertices might increase tour length unpredictably. Maintaining this property ensures that directly skipping vertices on the Eulerian path does not inflate the tour length, making approximation guarantees valid.
Other Approximation Techniques for Metric TSP
- Nearest Neighbor Heuristic: Simple but no constant factor approximation guarantee for metric TSP.
- 2-Approximation using MST: Doubling the MST edges and shortcutting yields a 2x approximation.
This is often a baseline but Christofides improves the factor to 1.5.
Interactive Example Consideration
An interactive visualization can help understand MST construction, odd vertex matching, and Eulerian path shortcuts dynamically. Tools like D3.js or p5.js visualize point sets, MST edges, matchings, and tours interactively, enabling learners to manipulate points and see immediate effects on approximations.
Summary
The Metric TSP restricted to Euclidean distances leverages the triangle inequality for strong approximation guarantees. Christofides algorithm remains the cornerstone with its elegant MST-plus-matching method assuring a 1.5-approximation ratio. Understanding its steps and seeing examples with corresponding diagrams are crucial for grasping the algorithm’s power and practical utility in routing and logistics problems.
For further learning, checking implementations and experimenting with visual tools complements theory with experiential insight.