Merge Sort Implementation: Classic Divide and Conquer Example with Python

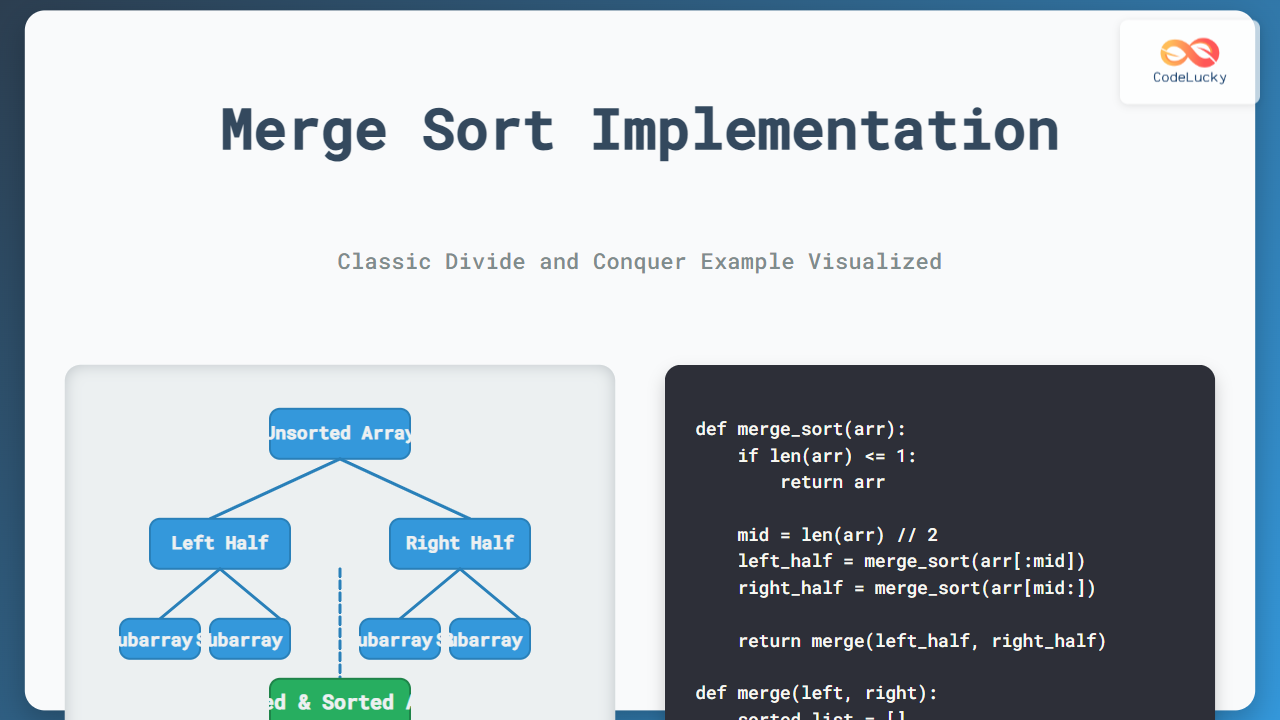
Sorting is one of the most fundamental problems in computer science, forming the building block for many advanced algorithms. Among the several sorting methods, Merge Sort stands out as a classic representation of the divide and conquer paradigm. It divides a problem into smaller subproblems, solves them recursively, and then merges the results into a complete solution.

What is Merge Sort?

Merge Sort is a stable, comparison-based sorting algorithm. It efficiently sorts elements by splitting an array into halves until each subarray has one element, and then merges these subarrays in sorted order. The beauty of Merge Sort lies in its reliance on the divide and conquer approach, which ensures a guaranteed time complexity of O(n log n).

Why is Merge Sort a Classic Divide and Conquer Example?

• Divide: Split the list into two halves.
• Conquer: Recursively sort both halves.
• Combine: Merge the sorted halves into a single sorted list.

Merge Sort Algorithm Step-by-Step

1. Take an unsorted array arr.
2. If the array has fewer than two elements, return it.
3. Recursively split the array into halves until single elements remain.
4. Merge the left and right halves in sorted order.

Python Implementation of Merge Sort

def merge_sort(arr):
    if len(arr) <= 1:
        return arr
    
    mid = len(arr) // 2
    left_half = merge_sort(arr[:mid])
    right_half = merge_sort(arr[mid:])
    
    return merge(left_half, right_half)

def merge(left, right):
    sorted_list = []
    i = j = 0
    
    while i < len(left) and j < len(right):
        if left[i] <= right[j]:
            sorted_list.append(left[i])
            i += 1
        else:
            sorted_list.append(right[j])
            j += 1
    
    sorted_list.extend(left[i:])
    sorted_list.extend(right[j:])
    
    return sorted_list

# Example
arr = [38, 27, 43, 3, 9, 82, 10]
print("Original array:", arr)
print("Sorted array using Merge Sort:", merge_sort(arr))

Program Output

Original array: [38, 27, 43, 3, 9, 82, 10]
Sorted array using Merge Sort: [3, 9, 10, 27, 38, 43, 82]

Visualizing the Process

The recursive splitting of arrays can be visualized as a binary tree of divisions.

Complexity Analysis of Merge Sort

• Time Complexity:
  • Best Case: O(n log n)
  • Average Case: O(n log n)
  • Worst Case: O(n log n)
• Space Complexity: O(n), due to auxiliary arrays used during merging.
• Sorting Stability: Merge Sort is stable, meaning it preserves the order of equal elements.

Practical Applications of Merge Sort

• Efficient sorting when dataset size is large and memory is not a major constraint.
• Useful in linked list sorting, since it does not require random access for efficient performance.
• Applied in external sorting algorithms where data does not fit into memory (e.g., sorting files on disk).

Interactive Example

Below is a simple interactive example in Python you can try:

# Try merging two sorted lists step by step
def step_merge(left, right):
    result, i, j = [], 0, 0
    while i < len(left) or j < len(right):
        print("Current Result:", result)
        if j == len(right) or (i < len(left) and left[i] <= right[j]):
            result.append(left[i])
            i += 1
        else:
            result.append(right[j])
            j += 1
    return result

print(step_merge([1, 4, 7], [2, 5, 8]))

Conclusion

Merge Sort is a textbook example of the divide and conquer strategy. While it uses more memory than some in-place algorithms like Quick Sort, its predictability and stability make it an excellent choice for large datasets and in scenarios where consistent O(n log n) performance is required.