Maximum Flow Problem: Ford-Fulkerson Algorithm Explained with Examples

The Maximum Flow Problem is a fundamental concept in graph theory and computer science, dealing with the optimal way to send flow through a network from a source to a sink while respecting capacity constraints. One of the most classic and widely studied approaches to solve this problem is the Ford-Fulkerson Algorithm. This article offers a detailed, step-by-step explanation of the algorithm, complete with examples and visualizations to help understand its workings thoroughly.

Table of Contents

What is the Maximum Flow Problem?

Given a directed graph where each edge has a capacity, the objective is to find the maximum amount of flow that can be sent from a specified source node to a sink node without exceeding the capacities on the edges. The flow must satisfy:

Capacity constraint: Flow on each edge cannot exceed the edge’s capacity.
Flow conservation: Except at the source and sink, the total flow entering a node must equal the flow leaving it.

Overview of the Ford-Fulkerson Algorithm

The Ford-Fulkerson method is an iterative approach that increases flow by finding augmenting paths in the residual graph until no more augmenting paths exist. The residual graph represents the remaining capacities of the edges after accounting for the current flow. The key concept is:

While there exists a path from source to sink in the residual graph with available capacity, push flow along that path.
Update the residual capacities accordingly.

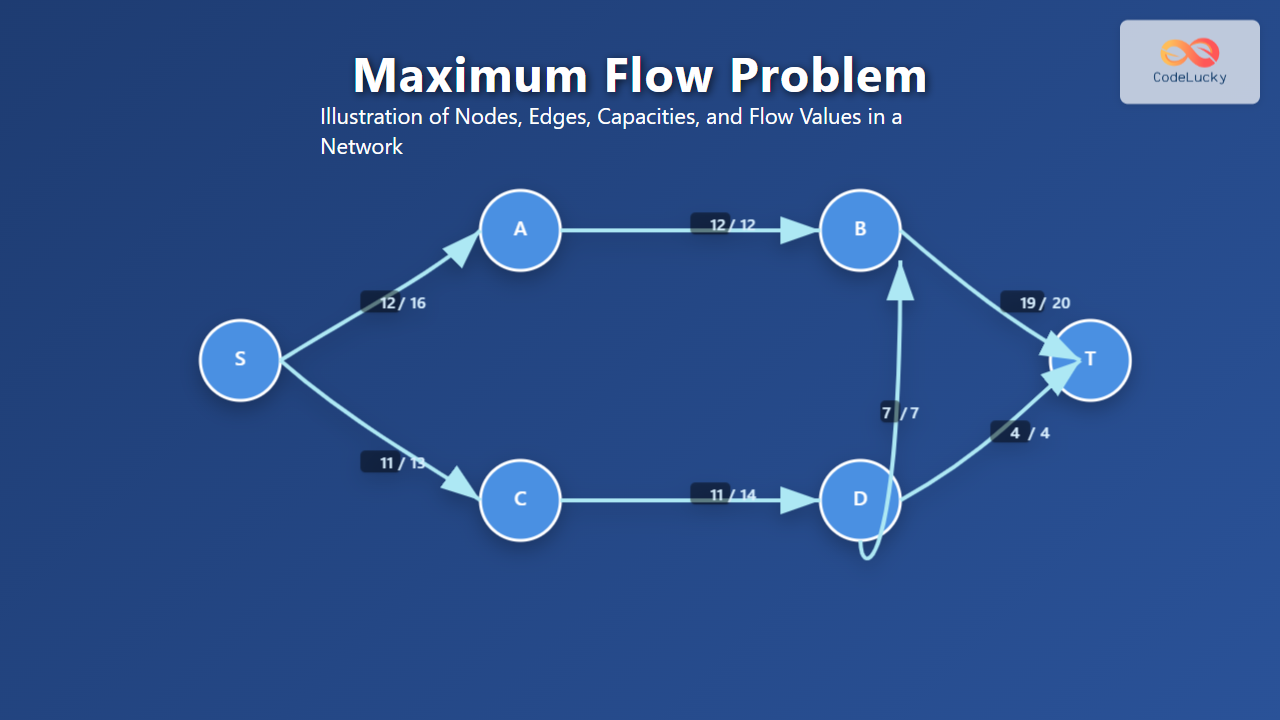
Above is a sample flow network with capacities labeled on each edge.

Step-by-Step Explanation

Initialize flow: Initially, set the flow on all edges to zero.
Construct residual graph: For each edge, if the flow is less than capacity, create a forward edge in the residual graph with capacity equal to remaining capacity. Also, create a backward edge to allow flow cancellation.
Find augmenting path: Use Depth-First Search (DFS) or Breadth-First Search (BFS) to find a path from source to sink in the residual graph with available capacity.
Update flow: Determine the minimum residual capacity along that path. Add this value to all forward edges in the path and subtract it from backward edges.
Repeat: Continue until no augmenting path exists.

Example Walkthrough

Consider the graph given above. Initially, all flows are zero.

First augmenting path: S → A → B → T

Capacities along the path: 16 (S→A), 12 (A→B), 20 (B→T)
Minimum capacity = 12
Send flow 12 along this path.

State update: Flow on edges S→A, A→B, B→T becomes 12.

Second augmenting path: S → C → D → T

Capacities: 13 (S→C), 14 (C→D), 4 (D→T)
Minimum capacity = 4
Send flow 4 along this path.

State update: Flow on S→C, C→D, D→T becomes 4.

Third augmenting path: S → C → D → B → T

Capacities: Remaining on S→C is 9 (13 – 4), C→D is 10 (14 – 4), D→B is 7, B→T is 8 (20 – 12)
Minimum capacity: 7
Send flow 7 along this path.

State update: Flow on S→C becomes 11, C→D becomes 11, D→B becomes 7, B→T becomes 19.

Algorithm Pseudocode


function fordFulkerson(graph, source, sink):
    initialize flow = 0
    while there exists a path P from source to sink in residual graph:
        find minimum capacity along path P (path_flow)
        for each edge (u,v) in P:
            reduce residual capacity of (u,v) by path_flow
            increase residual capacity of (v,u) by path_flow
        flow += path_flow
    return flow

Key Properties

The Ford-Fulkerson algorithm terminates if all capacities are integers, since each augmenting step increases the flow by at least one unit.
If capacities are irrational, the method might not terminate.
Time complexity depends on the method of finding augmenting paths (commonly O(E * max_flow) for basic DFS implementation).

Interactive Example (Concept)

Imagine an interactive flow network where the user can click edges to increase flow along augmented paths. As paths are found, flows animate updating. While this article cannot embed this interaction, this concept helps users visualize the iterative process.

Why Ford-Fulkerson? Practical Applications

This algorithm and the maximum flow problem have wide applications such as:

Network routing and bandwidth allocation
Project scheduling and resource allocation
Image segmentation in computer vision
Bipartite matching problems

Summary

The Ford-Fulkerson Algorithm provides a fundamental and intuitive method to solve the Maximum Flow Problem by repeatedly finding augmenting paths. It introduces key concepts like residual graphs and flow augmentation, which form the basis for more advanced algorithms like the Edmonds-Karp method. Understanding this algorithm is essential for work in network optimization and graph theory.