Matrix Chain Multiplication: Optimal Parenthesization Problem Explained with Examples

Matrix Chain Multiplication is a classic optimization problem in dynamic programming, often introduced in computer science courses to showcase how optimal substructure and overlapping subproblems can be leveraged for efficient computation. The problem asks:

Given a sequence of matrices to be multiplied, what is the most efficient way to parenthesize them so that the total number of scalar multiplications is minimized?

If we multiply matrices without considering the order, the number of operations can blow up unnecessarily. The goal is to find the optimal parenthesization that minimizes the cost.

Table of Contents

Understanding the Problem

Matrix multiplication is associative, meaning (AB)C = A(BC) in terms of result, but the cost differs due to the number of scalar multiplications required.

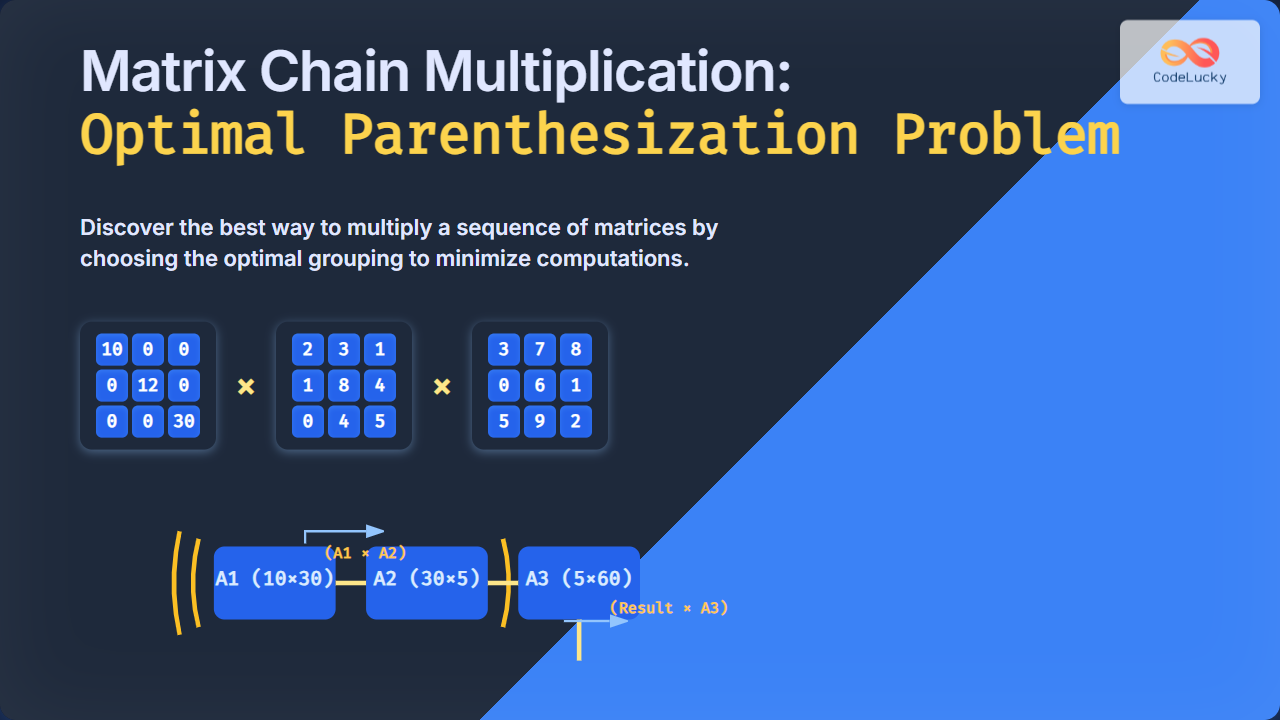
Let’s take an example:

Matrix A: 10 x 30
Matrix B: 30 x 5
Matrix C: 5 x 60

Two possible parenthesizations:

(AB)C
– Multiply A (10×30) with B (30×5): Cost = 10×30×5 = 1500
– Resulting matrix = 10×5
– Multiply with C (5×60): Cost = 10×5×60 = 3000
– Total = 4500 scalar multiplications
A(BC)
– Multiply B (30×5) with C (5×60): Cost = 30×5×60 = 9000
– Resulting matrix = 30×60
– Multiply with A (10×30): Cost = 10×30×60 = 18000
– Total = 27000 scalar multiplications

Clearly, (AB)C is better with only 4500 operations vs 27000. This illustrates why parenthesization matters.

Formal Problem Definition

Suppose we are given a chain of n matrices: A1, A2, A3, ..., An such that the dimension of matrix Ai is p[i-1] × p[i]. The task is to determine the optimal order of multiplication.

Goal: Minimize the total number of scalar multiplications required.

Dynamic Programming Approach

The brute-force approach of trying every possible parenthesization is exponential. Instead, we use dynamic programming by exploiting these properties:

Optimal Substructure: Choosing where to split the chain reduces the problem into two smaller subproblems.
Overlapping Subproblems: Many subproblems are solved repeatedly, making memoization or tabulation efficient.

Recursive Formula

If M[i][j] represents the minimum scalar multiplications required to compute matrices from Ai to Aj:

M[i][j] = min{ M[i][k] + M[k+1][j] + p[i-1] * p[k] * p[j] } for all i ≤ k < j

Algorithm Steps

Initialize M[i][i] = 0 (single matrix multiplication cost is zero).
Compute solutions for increasing chain lengths.
Store parenthesization choices for reconstruction.

Tabulation Example

Let’s solve the earlier example with dimensions array [10, 30, 5, 60].

p = [10, 30, 5, 60]
n = 3 (matrices)

M table (minimum multiplication cost):
M[1][1] = 0
M[2][2] = 0
M[3][3] = 0

For chain length = 2:
M[1][2] = 10*30*5 = 1500
M[2][3] = 30*5*60 = 9000

For chain length = 3:
M[1][3] = min(
  M[1][1] + M[2][3] + 10*30*60 = 0 + 9000 + 18000 = 27000,
  M[1][2] + M[3][3] + 10*5*60  = 1500 + 0 + 3000  = 4500
) = 4500

Optimal cost = 4500.

Python Implementation

Here is a complete dynamic programming solution in Python that also reconstructs the optimal parenthesization:


import sys

def matrix_chain_order(p):
    n = len(p) - 1
    M = [[0 for _ in range(n+1)] for _ in range(n+1)]
    S = [[0 for _ in range(n+1)] for _ in range(n+1)]

    for L in range(2, n+1):  # L = chain length
        for i in range(1, n-L+2):
            j = i + L - 1
            M[i][j] = sys.maxsize
            for k in range(i, j):
                cost = M[i][k] + M[k+1][j] + p[i-1]*p[k]*p[j]
                if cost < M[i][j]:
                    M[i][j] = cost
                    S[i][j] = k
    return M, S

def print_optimal_parens(S, i, j):
    if i == j:
        return f"A{i}"
    else:
        return "(" + print_optimal_parens(S, i, S[i][j]) + \
               print_optimal_parens(S, S[i][j]+1, j) + ")"

# Example usage
p = [10, 30, 5, 60]
M, S = matrix_chain_order(p)
print("Optimal cost:", M[1][len(p)-1])
print("Optimal parenthesization:", print_optimal_parens(S, 1, len(p)-1))

Output:


Optimal cost: 4500
Optimal parenthesization: ((A1A2)A3)

Visualizing Optimal Parenthesization

The optimal split can be represented as a binary tree where internal nodes represent multiplication operations:

Applications of Matrix Chain Multiplication

Compiler Design: Helps in query optimization in database systems (choosing join orders).
Linear Algebra Systems: Optimizing matrix operations in numerical computation libraries.
Computer Graphics: Efficiently applying transformations represented by matrix multiplication.
Dynamic Programming Education: Serves as a benchmark example of optimal substructure usage.

Conclusion

The Matrix Chain Multiplication problem elegantly demonstrates the power of dynamic programming. By breaking down the multiplication task into smaller subproblems, we achieve a polynomial-time solution for what was exponential with brute force. Understanding this algorithm not only helps in solving matrix problems but also enhances problem-solving techniques for optimization in compilers, databases, and scientific computing.