Longest Common Substring: Dynamic Programming String Problem with Examples

The Longest Common Substring (LCS) problem is one of the classical string problems in computer science and a standard application of Dynamic Programming. Unlike the Longest Common Subsequence problem, which does not require matching characters to be contiguous, the Longest Common Substring requires the matching segment to be continuous in both strings. This problem has direct applications in text processing, bioinformatics (DNA sequence matching), plagiarism detection, and file comparison.

Problem Definition

Given two strings str1 and str2, the Longest Common Substring problem asks us to find the length (and optionally the substring itself) of the longest sequence of characters that occurs in both strings contiguously.

Example:

str1 = "ABABC"
str2 = "BABCA"
Longest Common Substring = "BABC"
Length = 4

Naive Approach

A brute-force solution would be to generate all substrings of one string and check whether they occur in the other string. This leads to an O(n^3) complexity in the worst case, which is highly inefficient for larger inputs.

Dynamic Programming Approach

Dynamic Programming offers a much more efficient solution with O(n * m) time complexity where n and m are lengths of the two strings.

Core Idea

• Create a DP table dp[n+1][m+1] where dp[i][j] represents the length of the longest common substring that ends at str1[i-1] and str2[j-1].
• If str1[i-1] == str2[j-1], then dp[i][j] = dp[i-1][j-1] + 1.
• Else, dp[i][j] = 0, since substrings must be continuous.
• Track the maximum value across the table, which represents the length of the longest common substring.

Python Implementation

def longest_common_substring(str1, str2):
    n, m = len(str1), len(str2)
    dp = [[0] * (m + 1) for _ in range(n + 1)]
    max_len = 0
    end_index = 0  # to reconstruct substring
    
    for i in range(1, n + 1):
        for j in range(1, m + 1):
            if str1[i - 1] == str2[j - 1]:
                dp[i][j] = dp[i - 1][j - 1] + 1
                if dp[i][j] > max_len:
                    max_len = dp[i][j]
                    end_index = i
            else:
                dp[i][j] = 0
    
    # Extract substring
    longest_substr = str1[end_index - max_len:end_index]
    return max_len, longest_substr

# Example
print(longest_common_substring("ABABC", "BABCA"))

Output:

(4, 'BABC')

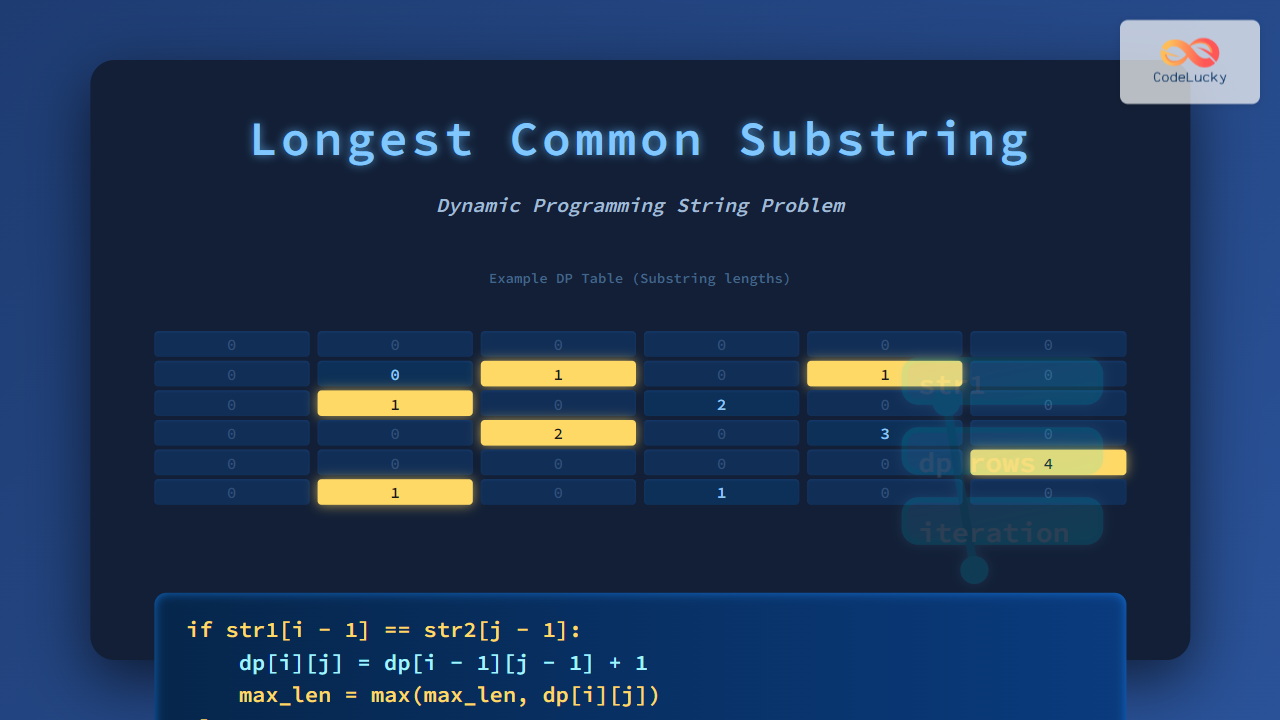
Visualizing the DP Table

For the example str1 = "ABABC" and str2 = "BABCA", below is a filled DP matrix (values represent length of matching substring ending at that index):

      A  B  A  B  C
   0  0  0  0  0  0
B  0  0  1  0  1  0
A  0  1  0  2  0  0
B  0  0  2  0  3  0
C  0  0  0  0  0  4
A  0  1  0  1  0  0

Maximum value 4 corresponds to substring "BABC".

Extracting the Substring

Besides finding the length, we can reconstruct the substring using the end_index and max_len stored during computation, ensuring we return the correct continuous segment.

Complexity Analysis

• Time Complexity: O(n * m) since each pair of characters is compared once.
• Space Complexity: O(n * m) for storing the DP table. This can be optimized to O(min(n,m)) by retaining only the previous row.

Optimized Space Version

def lcs_optimized(str1, str2):
    n, m = len(str1), len(str2)
    prev = [0] * (m + 1)
    max_len = 0
    end_index = 0

    for i in range(1, n + 1):
        curr = [0] * (m + 1)
        for j in range(1, m + 1):
            if str1[i - 1] == str2[j - 1]:
                curr[j] = prev[j - 1] + 1
                if curr[j] > max_len:
                    max_len = curr[j]
                    end_index = i
        prev = curr
    
    return max_len, str1[end_index - max_len:end_index]

Applications

• Plagiarism Detection: Finding common passages of text in two documents.
• Bioinformatics: Comparing DNA and protein sequences.
• File/Version Comparison: Determining similarities across different versions of files.
• Spell Checking: Matching input words with dictionary entries.

Conclusion

The Longest Common Substring problem is a fundamental string matching problem that demonstrates the power of Dynamic Programming. By using a DP matrix, we can efficiently find both the length and the actual substring in O(n*m) time. The algorithm is widely applicable across areas like computational biology, document similarity, version control, and more.

By understanding and mastering this algorithm, you gain a powerful toolset to solve real-world string problems where continuity of characters matters.