In computer science, randomized algorithms play a vital role in tackling complex problems efficiently. Among them, Las Vegas Algorithms are unique because they always produce a correct result, but the runtime depends on random choices during execution. This article explores the inner workings of Las Vegas Algorithms, compares them to Monte Carlo methods, and provides detailed examples with diagrams and interactive visuals.
What Are Las Vegas Algorithms?
A Las Vegas Algorithm is a type of randomized algorithm that guarantees correctness of the output but has a random runtime. Unlike Monte Carlo algorithms, which might deliver incorrect results within bounded runtimes, Las Vegas methods prioritize correctness over predictability of execution time.
- Correctness: Output is always guaranteed to be correct.
- Runtime Variability: Execution time varies depending on random states or sampling.
- Applications: Sorting, searching, computational geometry, optimization problems.
Monte Carlo vs Las Vegas Algorithms
| Aspect | Monte Carlo Algorithm | Las Vegas Algorithm |
|---|---|---|
| Correctness | Might give an incorrect result | Always gives the correct result |
| Runtime | Bounded / predictable | Randomized, can vary widely |
| Use Cases | Approximation & probability-based problems | Sorting, selection, exact computation |
Classic Example: Randomized QuickSort
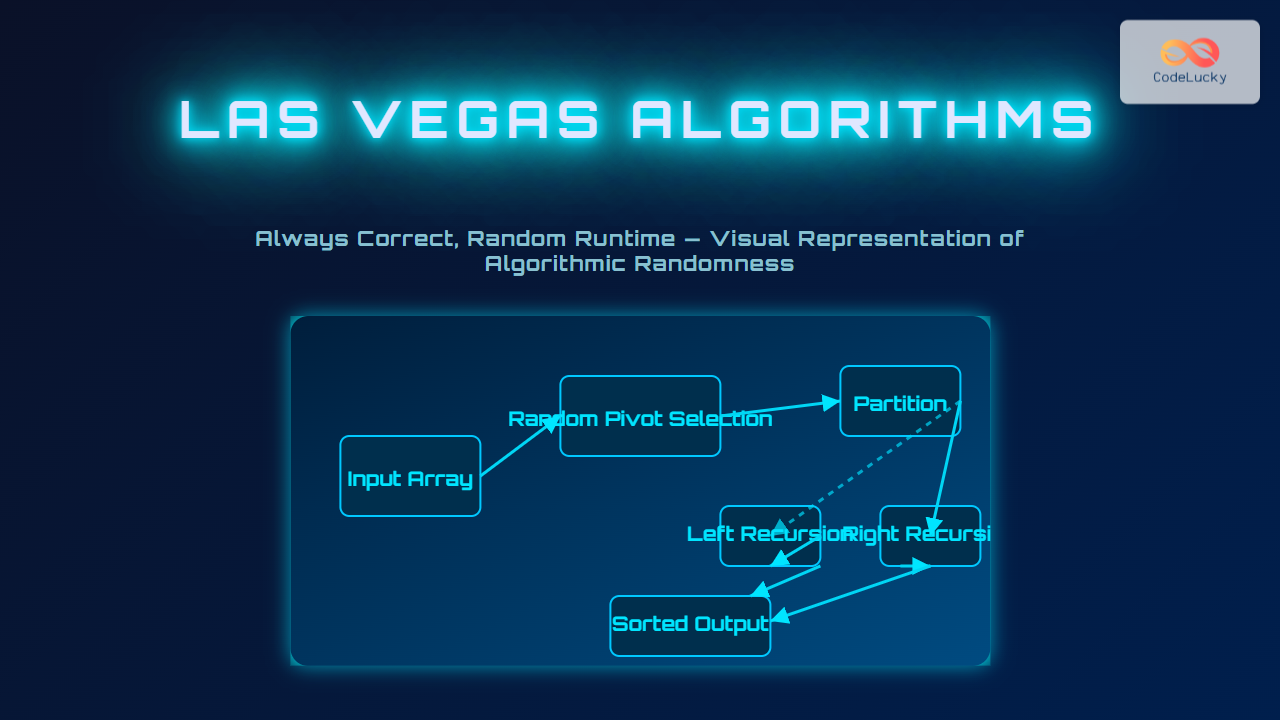
Randomized QuickSort is a well-known example of a Las Vegas algorithm. By randomly selecting a pivot each time instead of choosing it deterministically, the algorithm’s performance changes with different executions.
Even though the runtime depends on random pivot selection, the output is always a correctly sorted array. The expected runtime is O(n log n), but bad random choices can lead to O(n²) in some runs.
Example: Randomized Selection (QuickSelect)
The Randomized QuickSelect algorithm finds the k-th smallest element. It is always correct but runtime distribution varies.
import random
def randomized_partition(arr, low, high):
pivot_index = random.randint(low, high)
arr[pivot_index], arr[high] = arr[high], arr[pivot_index]
pivot = arr[high]
i = low
for j in range(low, high):
if arr[j] < pivot:
arr[i], arr[j] = arr[j], arr[i]
i += 1
arr[i], arr[high] = arr[high], arr[i]
return i
def randomized_select(arr, low, high, k):
if low == high:
return arr[low]
pivot = randomized_partition(arr, low, high)
if k == pivot:
return arr[pivot]
elif k < pivot:
return randomized_select(arr, low, pivot-1, k)
else:
return randomized_select(arr, pivot+1, high, k)
nums = [12, 3, 5, 7, 19, 26, 4]
k = 3
print("Kth smallest element:", randomized_select(nums, 0, len(nums)-1, k))
Output Example:
Kth smallest element: 5
Different runs may take more or fewer recursive calls because the pivot selection is randomized, but the result is always correct.
Interactive Visualization
To better understand variability, you can try the following snippet live in a Python environment. It will run QuickSelect multiple times and show how the runtime iterations vary while always yielding the correct answer.
import time
for _ in range(5):
start = time.time()
result = randomized_select(nums[:], 0, len(nums)-1, k)
print("Result:", result, "Time Taken:", time.time()-start)
Las Vegas Algorithm Runtime Distribution
This diagram shows how random inputs lead to variations in runtime. Unlike Monte Carlo algorithms, however, all paths guarantee correctness.
Applications of Las Vegas Algorithms
- Sorting: Randomized QuickSort avoids worst-case inputs more effectively than deterministic pivot strategies.
- Selection Problems: QuickSelect finds order statistics efficiently with expected linear time.
- Graph Algorithms: Randomized algorithms for minimum cut problems.
- Computational Geometry: Las Vegas techniques are used to find convex hulls and nearest neighbors.
Advantages and Limitations
- Advantages:
- Always produces correct output.
- Efficient on average compared to deterministic algorithms.
- Useful in bypassing adversarial inputs.
- Limitations:
- Execution time can vary unpredictably.
- May have pathological cases despite randomness.
Conclusion
Las Vegas Algorithms represent a fascinating balance between correctness and performance variability. They are widely applied in sorting, optimization, and geometry problems where randomization helps average-case efficiency without compromising correctness. While runtime is unpredictable, the guarantee of correctness makes them highly valuable in practical computing scenarios.