Kruskal’s Algorithm: Minimum Spanning Tree Using Union-Find Explained with Examples

Kruskal’s Algorithm is a classic greedy method used to find the Minimum Spanning Tree (MST) — a subset of edges in a weighted, undirected graph that connects all vertices without cycles and with the minimum possible total edge weight. This article explains Kruskal’s Algorithm in detail, focusing on an efficient implementation using the Union-Find (Disjoint Set) data structure. Clear examples, step-by-step visuals using mermaid diagrams, and code illustrations are included for deeper understanding.

What is a Minimum Spanning Tree?

A Minimum Spanning Tree of a graph ensures:

• All vertices (nodes) are connected.
• No cycles exist (which means it is a tree).
• The sum of the edge weights is the minimum possible.

This concept is essential in network design, clustering, and circuit design, among others.

Outline of Kruskal’s Algorithm

Kruskal’s algorithm builds the MST by:

1. Sorting all edges by their weights in ascending order.
2. Picking the smallest edge and checking if it forms a cycle with the already chosen edges.
3. If no cycle is formed, include the edge in MST; otherwise, discard it.
4. Repeat until MST includes all vertices or (V-1) edges.

The critical challenge is the cycle detection step, which is efficiently handled by the Union-Find data structure.

Union-Find Data Structure (Disjoint Set)

The Union-Find data structure supports two main operations efficiently:

• Find: Determine which subset a particular element is in. Useful for checking if two vertices belong to the same subset (cycle detection).
• Union: Join two subsets into a single subset.

This helps quickly decide if adding an edge links two vertices in the same component (cycle) or different ones (safe to add).

Step-by-Step Example

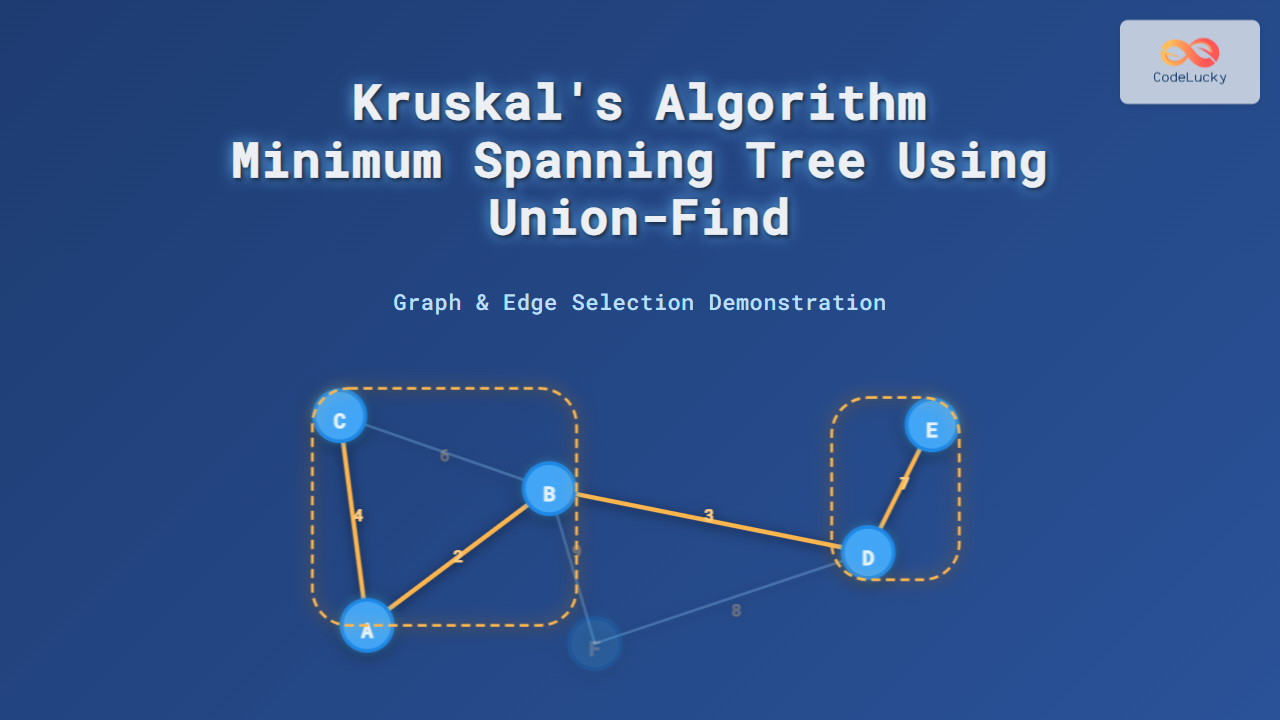
Consider the weighted graph below:

Edges sorted by weight: (A-C:2), (C-E:3), (A-B:4), (B-C:6), (D-E:7), (B-D:8), (C-D:9)

MST Construction using Union-Find

1. Edge A-C (2): No cycle, add edge. Union(A, C).
2. Edge C-E (3): No cycle, add edge. Union(C, E).
3. Edge A-B (4): No cycle, add edge. Union(A, B).
4. Edge B-C (6): Forms a cycle (A, B, C connected), discard.
5. Edge D-E (7): No cycle, add edge. Union(D, E).
6. At this point MST has 4 edges (V-1 = 5-1 = 4), so MST complete.

Code Snippet: Kruskal’s Algorithm with Union-Find

class UnionFind:
    def __init__(self, n):
        self.parent = list(range(n))
        self.rank = [0] * n

    def find(self, u):
        if self.parent[u] != u:
            self.parent[u] = self.find(self.parent[u])
        return self.parent[u]

    def union(self, u, v):
        rootU = self.find(u)
        rootV = self.find(v)
        if rootU != rootV:
            if self.rank[rootU] > self.rank[rootV]:
                self.parent[rootV] = rootU
            elif self.rank[rootU] < self.rank[rootV]:
                self.parent[rootU] = rootV
            else:
                self.parent[rootV] = rootU
                self.rank[rootU] += 1
            return True
        return False

def kruskal(n, edges):
    uf = UnionFind(n)
    mst = []
    edges.sort(key=lambda x: x[2])  # Sort edges by weight

    for u, v, w in edges:
        if uf.union(u, v):
            mst.append((u, v, w))
            if len(mst) == n - 1:
                break
    return mst

# Example usage:
edges = [
    (0, 1, 4), (0, 2, 2), (1, 2, 6), (1, 3, 8),
    (2, 3, 9), (2, 4, 3), (3, 4, 7)
]
n = 5
mst = kruskal(n, edges)
print("Edges in MST:", mst)

Interactive Visualization Suggestion

Implementing Kruskal’s algorithm step-by-step in an interactive web tool enhances learning. The tool can:

• Visualize the graph and edges.
• Sort edges by weight visually.
• Show Union-Find sets dynamically as edges are added.
• Highlight edges included in MST and discarded edges for cycles.

This interaction fosters intuition about MST formation and the critical role of cycle detection.

Complexity Analysis

• Sorting edges takes O(E log E), where E is number of edges.
• Union-Find operations (amortized) work in almost constant time O(α(V)), where α is the Inverse Ackermann function, very slow growing.
• Total runtime is dominated by sorting: O(E log E).

Summary

Kruskal’s Algorithm paired with Union-Find provides a highly efficient solution to find the Minimum Spanning Tree of a graph. It combines greedy edge selection with fast cycle detection via disjoint sets. This elegant approach works well for sparse graphs and offers clear conceptual and practical benefits for foundational graph problems in computer science.