Integer Multiplication: Karatsuba Algorithm Explained with Examples

Integer multiplication is one of the cornerstones of computer science and mathematics. While the grade-school method works fine for small numbers, it quickly becomes inefficient for very large integers. This is where the Karatsuba Algorithm comes into play — a fast multiplication algorithm based on the divide and conquer strategy, which reduces the time complexity significantly compared to the traditional method.

What is the Karatsuba Algorithm?

The Karatsuba Algorithm is a fast integer multiplication technique discovered by Anatoly Karatsuba in 1960. Unlike the naive multiplication method with a time complexity of \(O(n^2)\), the Karatsuba Algorithm reduces the complexity to approximately \(O(n^{1.585})\). It achieves this efficiency by recursively breaking down large numbers into smaller parts and reducing the required number of multiplications.

How Does It Work?

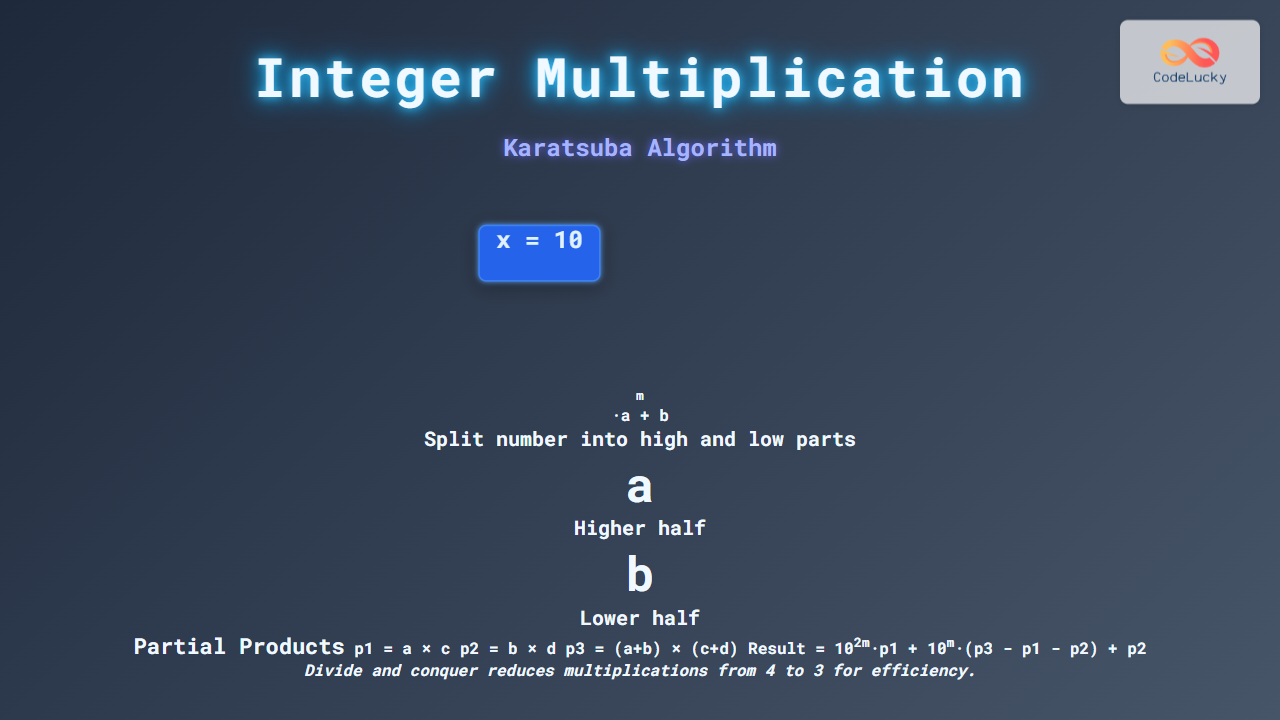
Suppose we want to multiply two large integers x and y, each represented with n digits. We split them into two halves:

x = 10^(m) * a + b  
y = 10^(m) * c + d

Where:

• a and c are the higher-order digits,
• b and d are the lower-order digits,
• m is roughly half the number of digits in the numbers.

Using the distributive property, we can express:

x * y = (10^m * a + b)(10^m * c + d)
      = 10^(2m) * (a * c) + 10^m * (a * d + b * c) + (b * d)

The naive approach requires four multiplications: a*c, a*d, b*c, and b*d. Karatsuba noticed that we can reduce this to only three multiplications by taking advantage of clever rearrangements:

p1 = a * c  
p2 = b * d  
p3 = (a + b) * (c + d)  
=> x * y = (10^(2m) * p1) + (10^m * (p3 - p1 - p2)) + p2

This trick saves one multiplication, which compounding recursively, yields a faster algorithm for large numbers.

Step-by-Step Example

Let’s multiply two numbers using Karatsuba Algorithm:

x = 1234, y = 5678
Split into two halves (m = 2 digits):
a = 12, b = 34
c = 56, d = 78

Step 1: p1 = a * c = 12 * 56 = 672  
Step 2: p2 = b * d = 34 * 78 = 2652  
Step 3: p3 = (a + b)(c + d) = (12+34)(56+78) = 46 * 134 = 6164  

Step 4: Combine results:
Result = (10^(4) * p1) + (10^2 * (p3 - p1 - p2)) + p2  
       = (10000 * 672) + (100 * (6164 - 672 - 2652)) + 2652  
       = 6720000 + 284000 + 2652  
       = 7006652

Verification: 1234 * 5678 = 7006652 ✅

Python Implementation

Here is a simple recursive implementation of the Karatsuba Algorithm in Python:

def karatsuba(x: int, y: int) -> int:
    # Base case
    if x < 10 or y < 10:
        return x * y

    # Calculate the size of the numbers
    n = max(len(str(x)), len(str(y)))
    m = n // 2

    # Split the numbers
    high_x, low_x = divmod(x, 10**m)
    high_y, low_y = divmod(y, 10**m)

    # Recursive multiplications
    p1 = karatsuba(high_x, high_y)
    p2 = karatsuba(low_x, low_y)
    p3 = karatsuba(high_x + low_x, high_y + low_y)

    return (10**(2*m) * p1) + (10**m * (p3 - p1 - p2)) + p2

# Example
print(karatsuba(1234, 5678))  # Output: 7006652

Complexity Analysis

By reducing four multiplications to three for each split, the corresponding recurrence relation is:

T(n) = 3T(n/2) + O(n)

Applying the Master Theorem, the time complexity of the Karatsuba Algorithm becomes:
O(n^log2(3)) ≈ O(n^1.585)

This is significantly faster than the classical O(n²) method, making it practical for cryptography, arbitrary-precision arithmetic, and large integer computations.

Advantages of Karatsuba Algorithm

• Faster than naive O(n²) multiplication for large integers.
• Forms the foundation for more advanced algorithms like Toom-Cook and Schönhage-Strassen.
• Used in many modern cryptographic libraries and big integer implementations.

Limitations

• Not efficient for small numbers (overhead of recursion).
• More complex to implement compared to the grade-school method.
• Advanced algorithms like FFT-based multiplication outperform Karatsuba for extremely large numbers.

Interactive Idea

To deepen understanding, you could implement an interactive visualization with Python or JavaScript where users input two numbers, and the app shows step-by-step recursive breakdown of p1, p2, and p3, with explanatory animations.

Conclusion

The Karatsuba Algorithm revolutionized integer multiplication by introducing a divide-and-conquer approach that significantly reduces complexity. It remains an essential technique in computer science, widely used in practical systems requiring efficient large integer computations. Understanding Karatsuba not only improves algorithmic knowledge but also lays the groundwork for exploring even faster multiplication techniques.