Jump Game Algorithm: Greedy Array Traversal Problem Explained with Examples

In algorithmic problem-solving, the Jump Game Algorithm is a classic greedy traversal problem often presented in competitive programming and technical interviews. It asks: Given an array of non-negative integers, where each element represents the maximum jump you can make from that position, determine if you can reach the last index starting from the first.

This problem is widely known for testing a programmer’s ability to optimize traversal strategies while balancing between greedy choices and dynamic programming insights. In this article, we will provide an exhaustive, SEO-friendly guide to the Jump Game problem with intuitive explanations, step-by-step Python examples, edge cases, diagrams, and complexity analysis.

Table of Contents

Problem Statement

You are given an array nums of length n. Each element nums[i] represents your maximum jump length from index i. You start at the first index (index 0). Your goal is to determine if you can reach the last index.


Example:
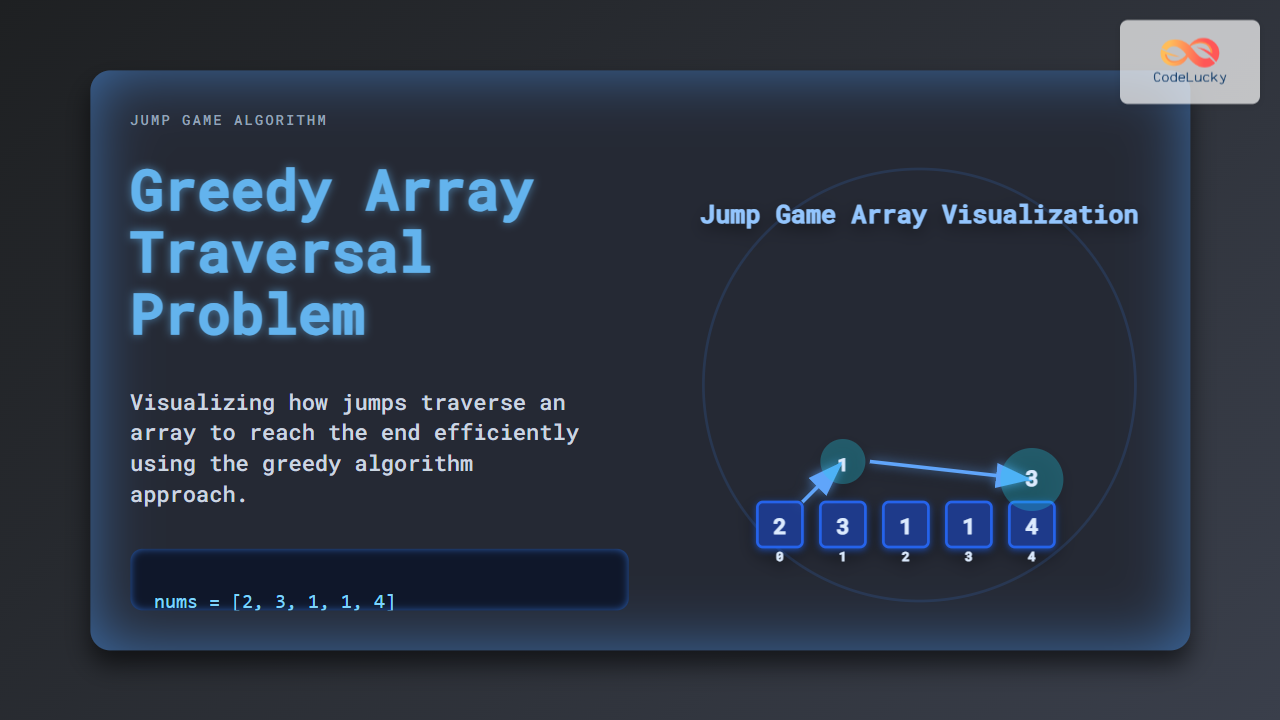
Input: nums = [2,3,1,1,4]
Output: true
Explanation: Start at index 0, jump 1 step to index 1, then jump 3 steps to the last index.

Visual Understanding of the Jump Game

Consider the array [2,3,1,1,4]. The element at index 0 allows jumping up to 2 steps. From index 1, you can jump up to 3 steps, enabling you to directly reach the last index.

Naive Approach: Backtracking

The most direct solution is to try every possible jump recursively from the current index until either you reach the end or conclude it’s impossible.


def can_jump_backtracking(nums, position=0):
    if position >= len(nums) - 1:
        return True
    furthest_jump = min(position + nums[position], len(nums) - 1)
    for next_pos in range(position + 1, furthest_jump + 1):
        if can_jump_backtracking(nums, next_pos):
            return True
    return False

nums = [2,3,1,1,4]
print(can_jump_backtracking(nums))  # True

While straightforward, this approach is exponential in time complexity and not feasible for larger inputs.

Greedy Algorithm: Optimized Solution

A greedy approach efficiently solves the Jump Game problem. The logic is simple:

Maintain the maxReach – the farthest index you can reach so far.
Iterate through the array, updating maxReach whenever possible.
If at any time the current index exceeds maxReach, you cannot proceed further.


def can_jump(nums):
    maxReach = 0
    for i, step in enumerate(nums):
        if i > maxReach:
            return False
        maxReach = max(maxReach, i + step)
        if maxReach >= len(nums) - 1:
            return True
    return True

# Example
print(can_jump([2,3,1,1,4]))  # True
print(can_jump([3,2,1,0,4]))  # False

This runs in O(n) time with O(1) space, making it highly efficient.

Visualizing the Greedy Process

Let’s trace [3,2,1,0,4]. At each index, we compute the farthest possible jump:

As shown above, you get stuck at index 3 since no further jump is possible.

Interactive Example

Run this Python snippet interactively to test different arrays:


def test_jump_game():
    while True:
        try:
            raw = input("Enter array (comma separated) or 'exit': ")
            if raw.strip().lower() == "exit":
                break
            nums = list(map(int, raw.split(",")))
            print("Can reach end?", can_jump(nums))
        except Exception as e:
            print("Invalid input, try again.")

# Uncomment to run
# test_jump_game()

Complexity Analysis

Backtracking: O(2^n), impractical for large inputs.
Greedy approach: O(n) time, O(1) space.

Variations of the Jump Game

The Jump Game problem has multiple variations worth exploring:

Jump Game II: Find the minimum number of jumps required to reach the last index.
Jump Game III: Start at any index and check if you can reach an index with value zero using jumps.

Conclusion

The Jump Game algorithm is an excellent example of how greedy strategies outperform brute-force solutions for traversal problems. Understanding it builds strong foundations in greedy programming, array manipulation, and algorithmic thinking that are frequently tested in coding interviews.

By mastering both the naive and optimized approaches, you will not only be able to solve this problem confidently but also recognize similar patterns in real-world algorithmic challenges.