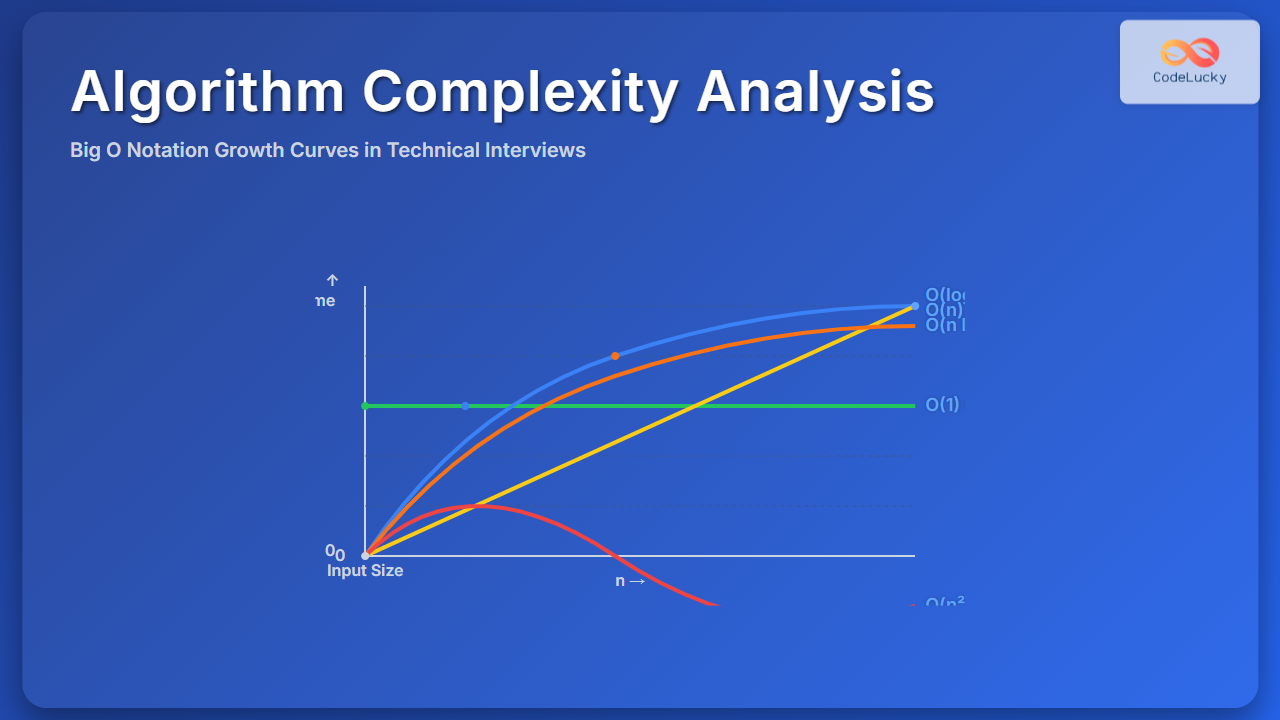
JavaScript Algorithms: Modern ES6+ Implementation Explained with Examples

JavaScript is no longer just a browser scripting language. With Node.js and modern ES6+ features, it has evolved into a powerful tool for solving computer science problems and implementing efficient algorithms. In this article, we will dive deep into JavaScript Algorithms using ES6+, explore step-by-step code examples, visualize processes with diagrams, and create interactive snippets that showcase how algorithms work in practice.

Table of Contents

Why Learn Algorithms in JavaScript?

Algorithms are the foundation of programming. Learning them in JavaScript is practical because:

JavaScript supports functional programming with map, reduce, and filter.
ES6+ features such as let, const, arrow functions, and classes make code more readable.
JavaScript runs on both client-side and server-side (via Node.js).
Many interviews and coding challenges use JavaScript for testing algorithmic skills.

Sorting Algorithms in JavaScript (ES6+)

Sorting is one of the most common algorithm problems. Let’s look at modern ES6+ implementations.

Bubble Sort (ES6+)


const bubbleSort = arr => {
  let n = arr.length;
  for (let i = 0; i < n - 1; i++) {
    for (let j = 0; j < n - i - 1; j++) {
      if (arr[j] > arr[j + 1]) {
        [arr[j], arr[j + 1]] = [arr[j + 1], arr[j]];
      }
    }
  }
  return arr;
};

console.log(bubbleSort([5, 2, 9, 1, 5, 6]));
// Output: [1, 2, 5, 5, 6, 9]

Quick Sort (Recursive with ES6 syntax)


const quickSort = arr => {
  if (arr.length <= 1) return arr;
  const pivot = arr[arr.length - 1];
  const left = [];
  const right = [];
  for (const el of arr.slice(0, -1)) {
    el < pivot ? left.push(el) : right.push(el);
  }
  return [...quickSort(left), pivot, ...quickSort(right)];
};

console.log(quickSort([10, 7, 8, 9, 1, 5]));
// Output: [1, 5, 7, 8, 9, 10]

Searching Algorithms

Linear Search


const linearSearch = (arr, target) => {
  for (let i = 0; i < arr.length; i++) {
    if (arr[i] === target) return i;
  }
  return -1;
};

console.log(linearSearch([3, 5, 7, 9, 11], 7));
// Output: 2

Binary Search (Efficient O(log n))


const binarySearch = (arr, target) => {
  let left = 0;
  let right = arr.length - 1;
  while (left <= right) {
    const mid = Math.floor((left + right) / 2);
    if (arr[mid] === target) return mid;
    arr[mid] < target ? left = mid + 1 : right = mid - 1;
  }
  return -1;
};

console.log(binarySearch([1, 3, 5, 7, 9, 11], 7));
// Output: 3

Recursion in JavaScript

Recursion is a fundamental concept where functions call themselves.

Factorial Using Recursion


const factorial = n => (n <= 1 ? 1 : n * factorial(n - 1));
console.log(factorial(5));
// Output: 120

Fibonacci Sequence


const fibonacci = n => (n <= 1 ? n : fibonacci(n - 1) + fibonacci(n - 2));
console.log(fibonacci(6));
// Output: 8

Graph Algorithms with ES6

Graphs are critical in representing relationships. Let’s explore BFS and DFS.

Breadth-First Search (BFS)


class Graph {
  constructor() {
    this.adjList = new Map();
  }

  addVertex(v) {
    this.adjList.set(v, []);
  }

  addEdge(v, w) {
    this.adjList.get(v).push(w);
  }

  bfs(start) {
    const visited = new Set();
    const queue = [start];
    while (queue.length) {
      const vertex = queue.shift();
      if (!visited.has(vertex)) {
        console.log(vertex);
        visited.add(vertex);
        queue.push(...this.adjList.get(vertex));
      }
    }
  }
}

const g = new Graph();
g.addVertex("A"); g.addVertex("B"); g.addVertex("C"); g.addVertex("D");
g.addEdge("A", "B"); g.addEdge("A", "C"); g.addEdge("B", "D"); g.addEdge("C", "D");

g.bfs("A");
// Output: A B C D

Depth-First Search (DFS)


Graph.prototype.dfs = function(start, visited = new Set()) {
  if (visited.has(start)) return;
  console.log(start);
  visited.add(start);
  for (const neighbor of this.adjList.get(start)) {
    this.dfs(neighbor, visited);
  }
};

g.dfs("A");
// Output: A B D C

Dynamic Programming Example

Memoized Fibonacci


const fibonacciDP = (n, memo = {}) => {
  if (n in memo) return memo[n];
  if (n <= 1) return n;
  memo[n] = fibonacciDP(n - 1, memo) + fibonacciDP(n - 2, memo);
  return memo[n];
};

console.log(fibonacciDP(10));
// Output: 55

Conclusion

Understanding JavaScript Algorithms with ES6+ makes you a more efficient and modern developer. From sorting and searching to recursion, graphs, and dynamic programming, JavaScript can elegantly express algorithmic logic with concise syntax. Use these implementations for practice, coding interviews, or real-world applications in your projects.