Interpolation Search: Improved Binary Search for Uniform Data

Searching efficiently in sorted data is one of the core problems in computer science. While binary search is famous for its logarithmic efficiency, it assumes a balanced split at the middle of the array every time. But what if our data is uniformly distributed? In such cases, Interpolation Search outperforms binary search by making a more intelligent guess about where the element might be. In this article, we will explore Interpolation Search in depth – its working principle, mathematics, efficiency, visual representation, and Python implementation with examples.

Table of Contents

What is Interpolation Search?

Interpolation Search is an improved search algorithm that uses the idea of predicting the probable position of the target element in a sorted array using interpolation formula, rather than always checking the middle like Binary Search. This makes it work much faster on uniformly distributed data.

Intuition Behind Interpolation Search

Suppose you are looking for page number 900 in a dictionary of 1000 pages. Instead of flipping to the middle (page 500) like Binary Search would, you would directly estimate the location near the end of the book since 900 is much closer to 1000 than 1. This is what Interpolation Search does mathematically.

Mathematics of Position Estimation

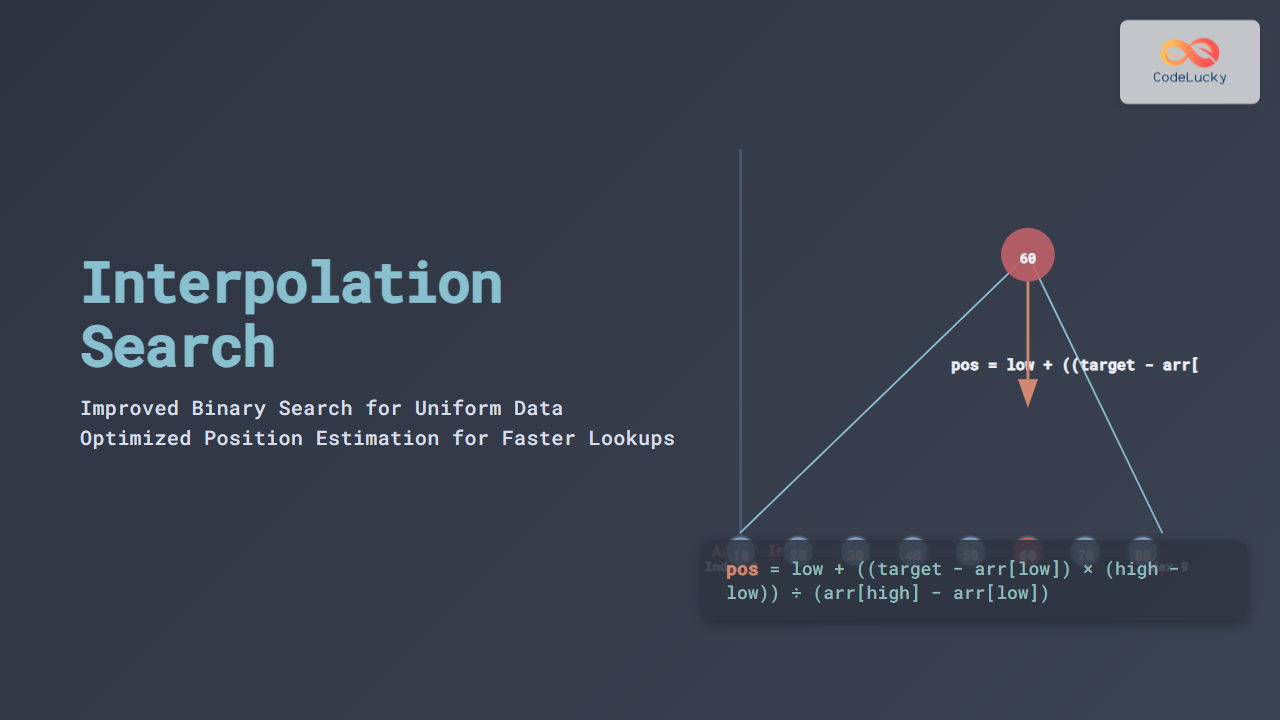
The position is estimated using linear interpolation:

pos = low + ((target - arr[low]) * (high - low)) // (arr[high] - arr[low])

Here:

low: starting index of search range
high: ending index of search range
arr[low] and arr[high]: boundary values
target: value being searched

Interpolation Search Algorithm Explained

Python Implementation of Interpolation Search


def interpolation_search(arr, target):
    low = 0
    high = len(arr) - 1

    while low <= high and target >= arr[low] and target <= arr[high]:
        # Estimate position
        pos = low + ((target - arr[low]) * (high - low)) // (arr[high] - arr[low])

        if arr[pos] == target:
            return pos
        elif arr[pos] < target:
            low = pos + 1
        else:
            high = pos - 1
    return -1


# Example usage
arr = [10, 20, 30, 40, 50, 60, 70, 80, 90, 100]
target = 70
result = interpolation_search(arr, target)
print(f"Element {target} found at index: {result}")

Output:


Element 70 found at index: 6

Visual Example: Step-by-Step Search

Consider searching for 60 in the sorted array [10,20,30,40,50,60,70,80,90,100].

Complexity Analysis of Interpolation Search

Best Case: O(1) (direct hit)
Average Case: O(log log n) for uniformly distributed data
Worst Case: O(n) when data is highly skewed or not uniform

Binary Search vs Interpolation Search

Binary Search is more reliable for arbitrary sorted data, while Interpolation Search excels when distribution is uniform.

Practical Applications

Searching for records in ID-based databases with uniform key distribution.
Lookup in large phone directories or sorted files.
Efficient search in numeric datasets like sensor logs or time-stamped readings.

Interactive Example (Try Yourself)

Run this snippet in Python to experiment :


arr = list(range(0, 1001, 10))  # Uniform array: [0, 10, 20, ... 1000]
target = int(input("Enter number to search (0-1000, multiple of 10): "))
result = interpolation_search(arr, target)
if result != -1:
    print(f"Found {target} at index {result}")
else:
    print("Not found")

Conclusion

Interpolation Search is a powerful variation of Binary Search that predicts the position of the target using interpolation. While its average performance on uniform data is excellent (O(log log n)), one must be cautious as it can degrade to linear time on skewed datasets. Therefore, it is best used in environments where data is evenly distributed. For general-purpose applications, Binary Search is safer, but for uniform datasets, Interpolation Search can be significantly faster.