Sorting is a fundamental concept in computer science, and understanding different sorting algorithms is important for both theory and practice. One of the simplest yet effective algorithms is the Insertion Sort Algorithm. As the name suggests, it works by building a sorted array one element at a time. Though not as fast as advanced algorithms like Quick Sort or Merge Sort, insertion sort holds its ground with simplicity, low overhead, and usefulness in real-world scenarios such as sorting small datasets or nearly-sorted data.
What is the Insertion Sort Algorithm?
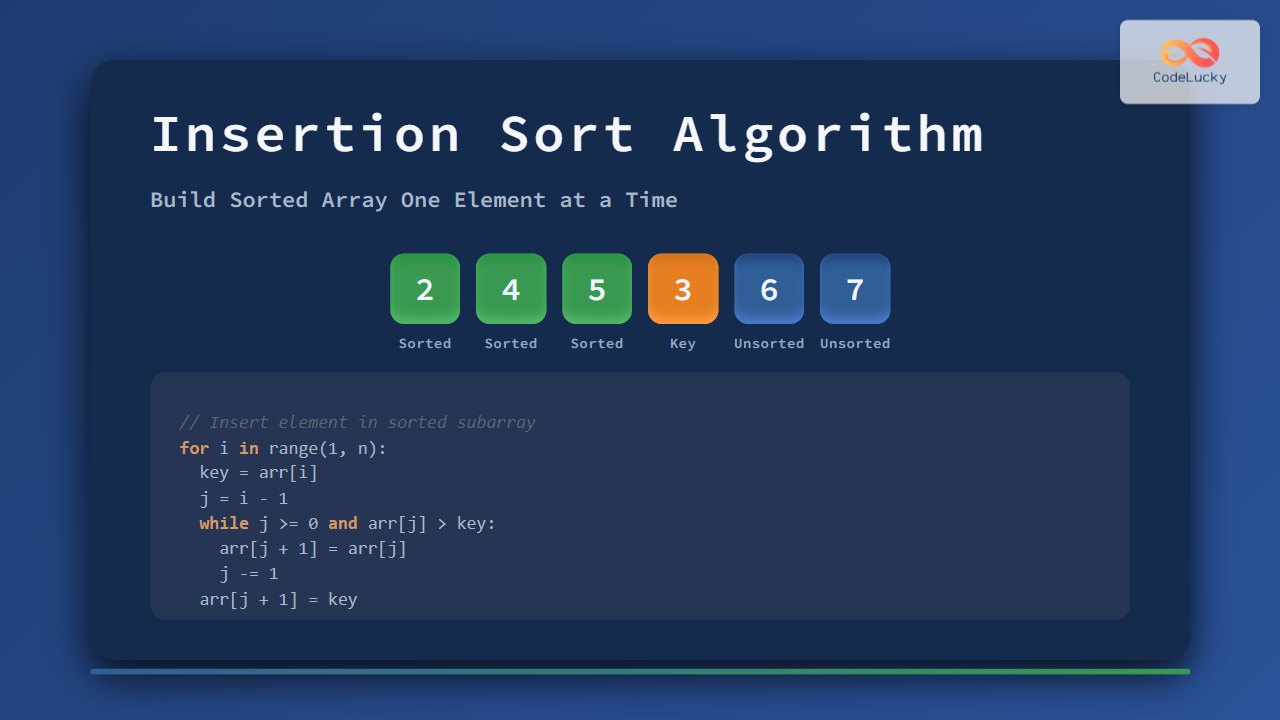
The insertion sort algorithm works in a way similar to how people arrange playing cards in their hands. You start with one card (assumed sorted) and then insert the next card into the correct position among the already sorted ones. This continues until all cards (array elements) are in sorted order.
How Insertion Sort Works Step-by-Step
- Start with the first element as a sorted subarray.
- Pick the next element from the unsorted part of the array.
- Compare it with elements in the sorted subarray and find its correct position.
- Shift all larger elements one position to the right to make space.
- Insert the element into its correct spot.
- Repeat until all elements are placed in the sorted order.
Example Walkthrough
Consider the array:
[5, 2, 4, 6, 1, 3]Step 1: First element [5] is considered sorted.
Step 2: Next element is 2. Compare with 5. Since 2 < 5, shift 5 to the right and insert 2 before it. Array becomes:
[2, 5, 4, 6, 1, 3]Step 3: Next element is 4. Compare with sorted (2,5). Insert 4 between 2 and 5. Array becomes:
[2, 4, 5, 6, 1, 3]Step 4: Next element is 6. It’s already bigger than all, so stays in place.
[2, 4, 5, 6, 1, 3]Step 5: Next element is 1. It is smaller than all. Shift (2,4,5,6) to the right and insert 1:
[1, 2, 4, 5, 6, 3]Step 6: Last element is 3. It goes between 2 and 4. Array becomes fully sorted:
[1, 2, 3, 4, 5, 6]Python Implementation of Insertion Sort
Let’s look at the Python code for insertion sort:
def insertion_sort(arr):
for i in range(1, len(arr)):
key = arr[i]
j = i - 1
# Move elements greater than key to one position ahead
while j >= 0 and key < arr[j]:
arr[j + 1] = arr[j]
j -= 1
arr[j + 1] = key
return arr
# Example usage
arr = [5, 2, 4, 6, 1, 3]
print("Original:", arr)
sorted_arr = insertion_sort(arr)
print("Sorted:", sorted_arr)
Output:
Original: [5, 2, 4, 6, 1, 3]
Sorted: [1, 2, 3, 4, 5, 6]
Visualizing Shifts and Insertions
Insertion Sort Complexity
- Best Case (Already Sorted): O(n)
- Worst Case (Reversed Order): O(n²)
- Average Case: O(n²)
- Space Complexity: O(1), since it’s in-place.
Although O(n²) seems inefficient, insertion sort performs extremely well for small datasets or when data is nearly sorted, making it practical in hybrid algorithms.
When to Use Insertion Sort
- For small datasets where simplicity is preferred over complexity.
- When the input is already “almost sorted.”
- In hybrid algorithms (like Timsort used in Python) as a fallback for small partitions.
Interactive Understanding
Try hand-tracing this algorithm with a small list of numbers. Write them on paper, pick one element at a time, and insert it into the right place in the partially sorted section. This exercise gives a better intuitive feel of how insertion sort works.
Key Takeaways
- Insertion Sort is simple, intuitive, and efficient for small or nearly sorted data.
- It works exactly like sorting playing cards in hand.
- Its time complexity is O(n) in the best case, O(n²) in the worst and average case.
- Low overhead and in-place sorting make it useful in specific scenarios.
Understanding insertion sort provides a foundation for grasping more complex sorting algorithms. By building one element at a time, you experience the most natural way of sorting, directly connecting theory with hands-on practice.