In the fascinating world of graph theory, understanding how to compare graph structures efficiently is crucial for many applications—from chemistry and pattern recognition to social network analysis. One key concept that emerges in such comparisons is graph isomorphism. But what exactly is graph isomorphism, why is it important, and how do we determine if two graphs are isomorphic? This detailed article explores these questions, provides clear visual examples, and dives into practical methods for testing graph equivalence.
What Is Graph Isomorphism?
Graph isomorphism is a concept that determines whether two graphs are essentially the same, even if their vertices or edges are labeled or arranged differently. Two graphs G1 = (V1, E1) and G2 = (V2, E2) are isomorphic if there exists a one-to-one correspondence (bijection) between their vertex sets V1 and V2 such that any edge (u, v) in G1 exists if and only if the corresponding edge (f(u), f(v)) exists in G2, where f is the bijection function.
In simpler terms, two graphs are isomorphic if one can be transformed into the other by just renaming vertices without changing the connectivity.
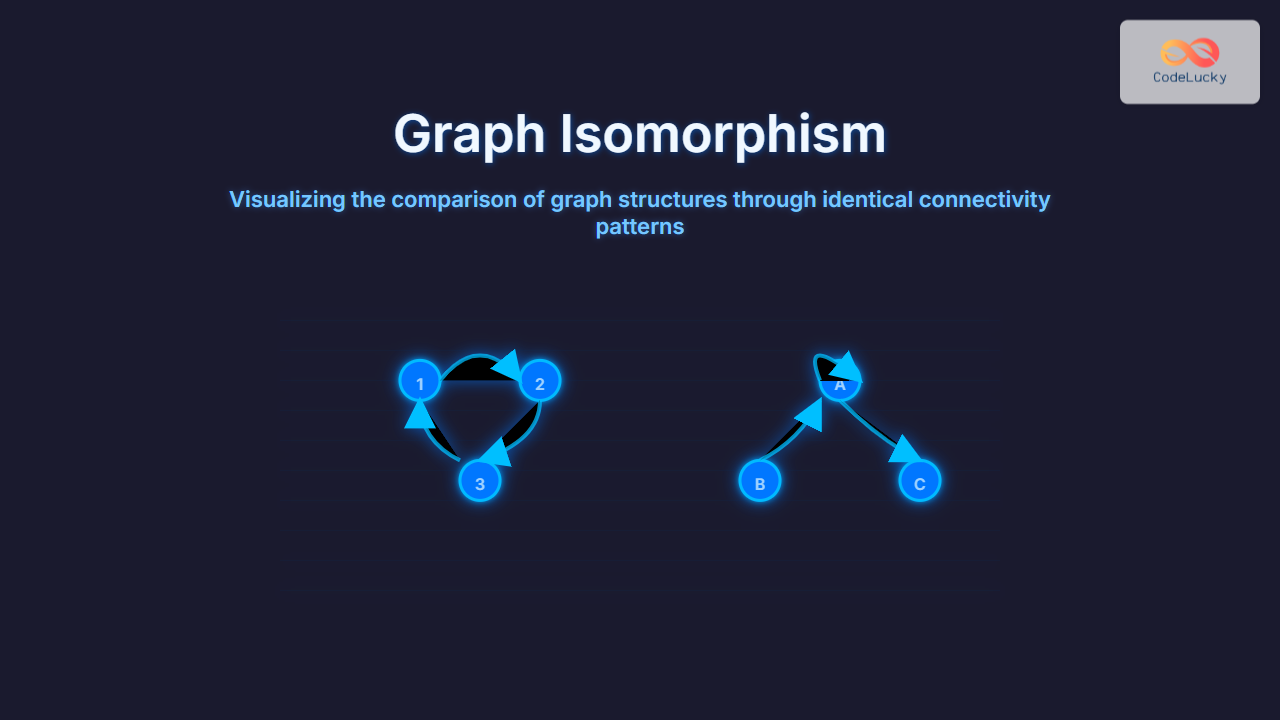
Here, Graph G1 and Graph G2 visually have different vertex labels and layout but the same connectivity pattern, so they are isomorphic.
Why Is Graph Isomorphism Important?
- Pattern Recognition: Checking molecular structures in chemistry or similar patterns in networks.
- Network Theory: Identifying identical subnetworks or duplicate structures in social or computer networks.
- Database Query: Graph databases use isomorphism to match query graphs against stored graphs.
- Optimization: Recognizing equivalent graph states may reduce computational effort in algorithms.
Formal Definition and Properties
Formally, graphs G1 = (V1, E1) and G2 = (V2, E2) are isomorphic if there exists a bijection function \( f: V1 \to V2 \) such that:
- For any \( u, v \in V1 \), \( (u,v) \in E1 \) if and only if \( (f(u), f(v)) \in E2 \).
- The function \( f \) preserves adjacency and non-adjacency.
Properties to note:
- Isomorphism is an equivalence relation (reflexive, symmetric, transitive).
- Vertex degrees are preserved under isomorphism.
- Number of edges and connectivity patterns remain identical.
Example: Checking Graph Isomorphism
Consider two simple undirected graphs:
To determine if they are isomorphic, the steps include:
- Compare vertex counts: Both have 3 vertices.
- Compare edge counts: Both have 3 edges.
- Compare degree sequences: For example, vertices in both graphs have degrees 2, 2, and 2.
- Try to find a bijection: Map Vertex 1 to a, 2 to b, 3 to c, and check if edges correspond.
Since all these criteria match perfectly, the graphs are isomorphic.
Common Algorithms to Test Graph Isomorphism
The graph isomorphism problem is computationally challenging, but several practical approaches exist:
- Naive brute-force: Test all possible vertex mappings (impractical for large graphs due to factorial complexity).
- Backtracking algorithms: Incrementally build vertex correspondences, backtracking on conflicts.
- Refinement techniques: Use vertex invariants like degree sequences, color refinement, and Weisfeiler-Lehman tests for pruning.
- VF2 algorithm: A well-known recursive search approach with backtracking optimized for node compatibility.
Interactive Visualization Example
The following Mermaid diagrams illustrate two directed graphs side by side. Interactive exploration through renaming vertices can help users better grasp isomorphism visually.
Practical Tips for Implementing Graph Isomorphism Check in Code
When implementing graph isomorphism checks programmatically:
- Start with quick checks: Compare number of vertices, edges, and degree distributions.
- Apply canonical labeling techniques to reduce graphs to standard forms and compare.
- Use libraries or existing algorithms (like NetworkX in Python which has an isomorphism module).
- Test on smaller graphs first to ensure correctness.
Conclusion
Graph isomorphism is a fundamental problem in graph theory that asks whether two graphs share the same structure, regardless of vertex naming. Visualizing these graphs through diagrams or software tools helps understand the concept deeply. Despite the complexity, many efficient algorithms exist for practical cases, making graph isomorphism checks feasible and valuable for numerous computer science and real-world problems.
Understanding the theory, combining formal checks with visual intuition, enables developers and researchers to harness graph isomorphism insights effectively.