Generate All Permutations: Backtracking String Combinations Explained with Examples

Generating all permutations of a string is a classic problem in computer algorithms. It is commonly solved using a technique called backtracking. Backtracking is a systematic way of exploring all possible solutions to a problem by building candidates step by step and eliminating the ones that fail to satisfy conditions. In this article, we will deeply explore how to generate all permutations of a string using backtracking with practical examples, diagrams, and Python code implementations.

Table of Contents

What is a String Permutation?

A permutation of a string is a rearrangement of its characters. For example, for the string "ABC", the permutations are:

If a string has n characters, the total number of permutations is n!. For instance, a 3-character string has 3! = 6 permutations.

Understanding Backtracking for Permutations

Backtracking works by fixing each character at a given position and recursively permuting the remaining characters. Once all possibilities for one fixed position are explored, it “backtracks” and tries other options. Think of it as a depth-first search (DFS) through all possible string arrangements.

Algorithm Steps

Choose a character to fix at the current index.
Swap it with the character at the current index.
Recursively call the function on the rest of the characters.
Backtrack (undo the swap) to restore the original string and try another possibility.

Python Implementation


def permute(string, left, right, results):
    if left == right:
        results.append("".join(string))
    else:
        for i in range(left, right + 1):
            # swap
            string[left], string[i] = string[i], string[left]
            permute(string, left + 1, right, results)
            # backtrack (undo swap)
            string[left], string[i] = string[i], string[left]

# Driver code
s = "ABC"
results = []
permute(list(s), 0, len(s) - 1, results)

print("All permutations of", s, ":")
print(results)

Output:

All permutations of ABC :
['ABC', 'ACB', 'BAC', 'BCA', 'CBA', 'CAB']

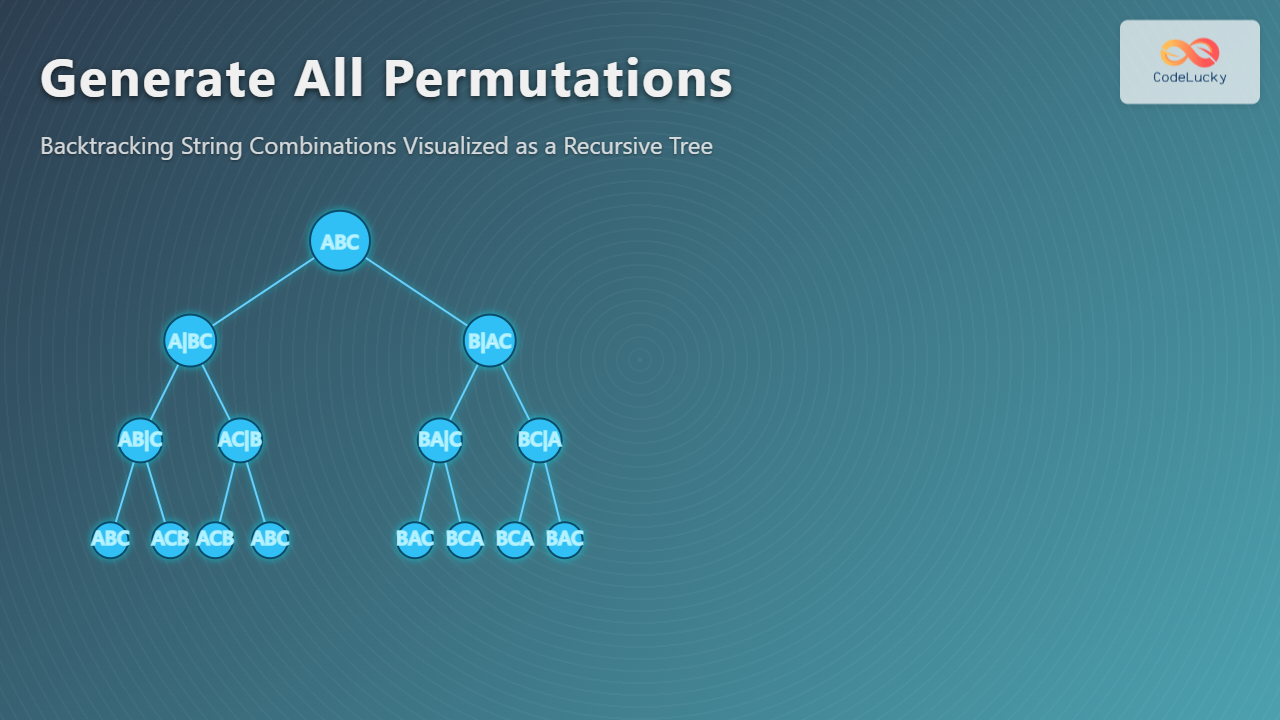
Visualizing Backtracking Steps

The recursive calls form a permutation tree where each branch represents a swap leading to a new arrangement.

Permutations of Strings with Duplicate Characters

When a string has duplicate characters, simple backtracking might generate duplicate permutations. To handle this, we can use a set or sort the input and skip duplicate characters while recursing.


def permute_unique(string, left, right, results):
    if left == right:
        results.add("".join(string))
    else:
        seen = set()
        for i in range(left, right + 1):
            if string[i] not in seen:
                seen.add(string[i])
                string[left], string[i] = string[i], string[left]
                permute_unique(string, left + 1, right, results)
                string[left], string[i] = string[i], string[left]

s = "AAB"
results = set()
permute_unique(list(s), 0, len(s) - 1, results)
print("Unique permutations:", results)

Output:

Unique permutations: {'ABA', 'BAA', 'AAB'}

Complexity Analysis

Time Complexity: The algorithm generates n! permutations, and each takes O(n) time to build, so overall complexity is O(n × n!).
Space Complexity: O(n) due to recursion depth, plus O(n!) storage when collecting all permutations.

Interactive Example

You can try generating permutations interactively in Python:


user_input = input("Enter a string: ")
results = []
permute(list(user_input), 0, len(user_input) - 1, results)
print("All permutations:")
for p in results:
    print(p)

Practical Applications

Cryptography: Brute-forcing keys by trying permutations.
Puzzle Solving: Backtracking problems like Sudoku and word jumbles.
Combinatorics: Generating all possible arrangements for testing.
Search Problems: Pathfinding in mazes or sequence ordering tasks.

Conclusion

Backtracking is an elegant and powerful technique to solve permutation generation problems. By systematically fixing characters, exploring recursive branches, and backtracking, we can explore all valid string combinations. Understanding this algorithm not only helps in academic learning but also builds a foundation for solving advanced backtracking and combinatorial problems.