Floyd-Warshall Algorithm: All-Pairs Shortest Path Solution Explained with Examples

The Floyd-Warshall Algorithm is a fundamental all-pairs shortest path algorithm in computer science. It leverages dynamic programming to compute shortest paths between every pair of nodes in a weighted graph. Unlike Dijkstra’s Algorithm, which typically solves single-source shortest paths, the Floyd-Warshall Algorithm efficiently handles all vertex pairs in a single run.

What is the Floyd-Warshall Algorithm?

The Floyd-Warshall Algorithm is a graph optimization algorithm that determines the shortest path between all pairs of vertices in a weighted graph. It can handle positive as well as negative weights (but not negative weight cycles).

The central idea is to iteratively improve the distance between two nodes by checking whether a path through an intermediate vertex offers a shorter path.

Algorithm Intuition

Consider three vertices i, j, and an intermediate vertex k. If the path i → k → j is shorter than the direct known path i → j, then we update the shortest known path to be i → k → j. By iterating over all vertices as potential intermediates, we refine the distance matrix until it contains the shortest distances between all pairs.

The Recurrence Relation

Mathematically, the algorithm is defined as:

D[k][i][j] = min(D[k-1][i][j], D[k-1][i][k] + D[k-1][k][j])

Where D[k][i][j] represents the shortest distance from vertex i to vertex j using only the first k vertices as intermediates.

Step-by-Step Example

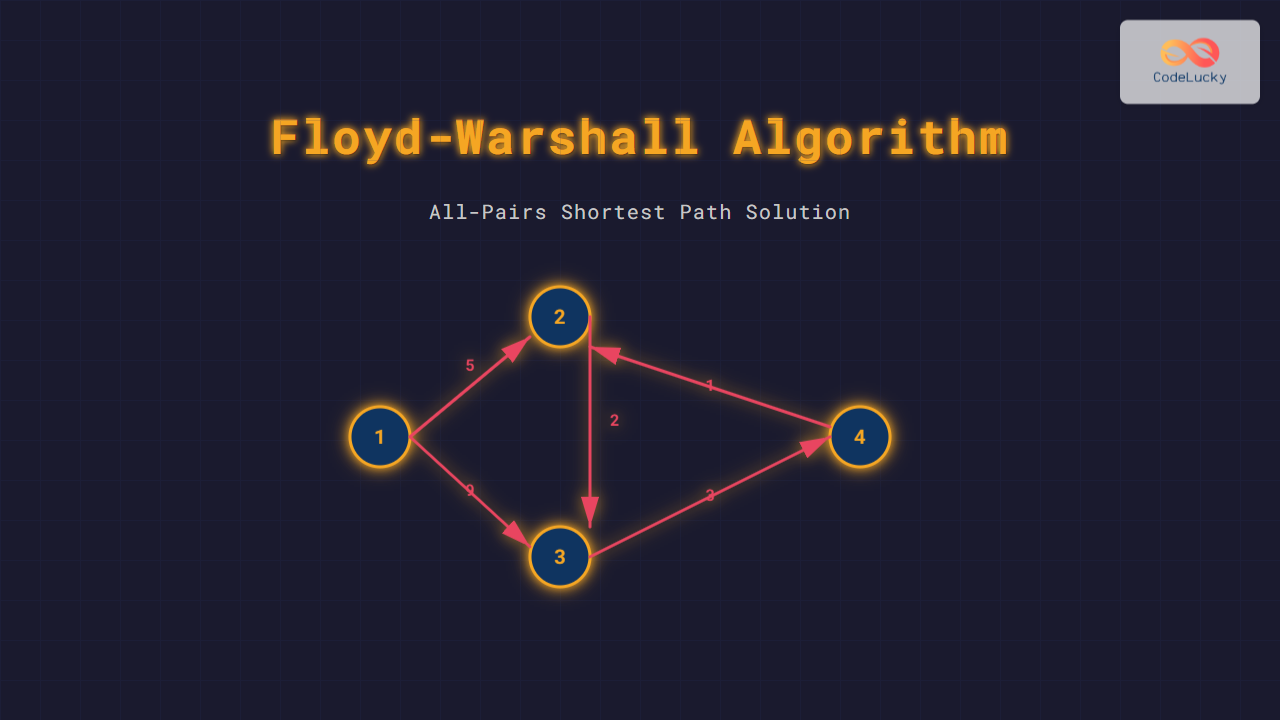
Let’s walk through an example graph with 4 vertices:

Initial adjacency matrix (∞ denotes no direct edge):

    1   2   3   4
1 [ 0   5   9  ∞ ]
2 [ ∞   0   2  ∞ ]
3 [ ∞  ∞   0   3 ]
4 [ ∞   1  ∞   0 ]

After running the Floyd-Warshall steps, the shortest path matrix becomes:

    1   2   3   4
1 [ 0   5   7  10 ]
2 [ ∞   0   2   5 ]
3 [ ∞   4   0   3 ]
4 [ ∞   1   3   0 ]

Python Implementation

Here is a clean, copy-paste-ready Python code for solving all-pairs shortest paths using Floyd-Warshall:

INF = float('inf')

def floyd_warshall(graph):
    n = len(graph)
    dist = [[graph[i][j] for j in range(n)] for i in range(n)]
    
    for k in range(n):
        for i in range(n):
            for j in range(n):
                if dist[i][k] + dist[k][j] < dist[i][j]:
                    dist[i][j] = dist[i][k] + dist[k][j]
    
    return dist

# Example usage
graph = [
    [0, 5, 9, INF],
    [INF, 0, 2, INF],
    [INF, INF, 0, 3],
    [INF, 1, INF, 0]
]

result = floyd_warshall(graph)

for row in result:
    print(row)

Interactive Example

Try modifying the graph in the code above and running it to see how the shortest path matrix changes in real-time. This is a great way to understand the dynamic programming approach of Floyd-Warshall.

Complexity Analysis

• Time Complexity: O(V³), as the algorithm involves three nested loops where V is the number of vertices.
• Space Complexity: O(V²), due to the distance matrix storing shortest paths between every pair.

Applications of Floyd-Warshall

The Floyd-Warshall Algorithm has real-world importance in many fields:

• Network routing protocols for computing optimal paths between all nodes.
• Urban traffic planning, determining shortest driving/walking times between all intersections.
• Computational biology for finding evolutionary distances between multiple species.
• AI pathfinding in games where all pairs of shortest paths might be needed ahead of time.

Handling Negative Cycles

While Floyd-Warshall can handle negative weights, it cannot handle graphs with negative cycles. If dist[i][i] < 0 for any vertex i after execution, it indicates the presence of a negative cycle.

Key Takeaways

• Floyd-Warshall solves the all-pairs shortest path problem.
• It uses dynamic programming to iteratively refine shortest distances.
• Works with negative edge weights but fails with negative cycles.
• Has O(V³) time complexity, making it suitable for dense graphs with fewer vertices.

The Floyd-Warshall Algorithm remains one of the most elegant shortest-path algorithms, thanks to its simplicity, mathematical beauty, and power in solving all-pairs problems where other algorithms would be less efficient or more complex.