The RADIANS function in Excel is a powerful mathematical tool that converts angle measurements from degrees to radians. This essential function is crucial for trigonometric calculations, engineering applications, and advanced mathematical modeling in spreadsheets.
What is the Excel RADIANS Function?
The RADIANS function is a built-in Excel function that belongs to the Math and Trigonometry category. It takes an angle measured in degrees and converts it to its equivalent value in radians. This conversion is fundamental for many mathematical calculations, especially when working with trigonometric functions like SIN, COS, and TAN.
RADIANS Function Syntax
The syntax for the RADIANS function is straightforward:
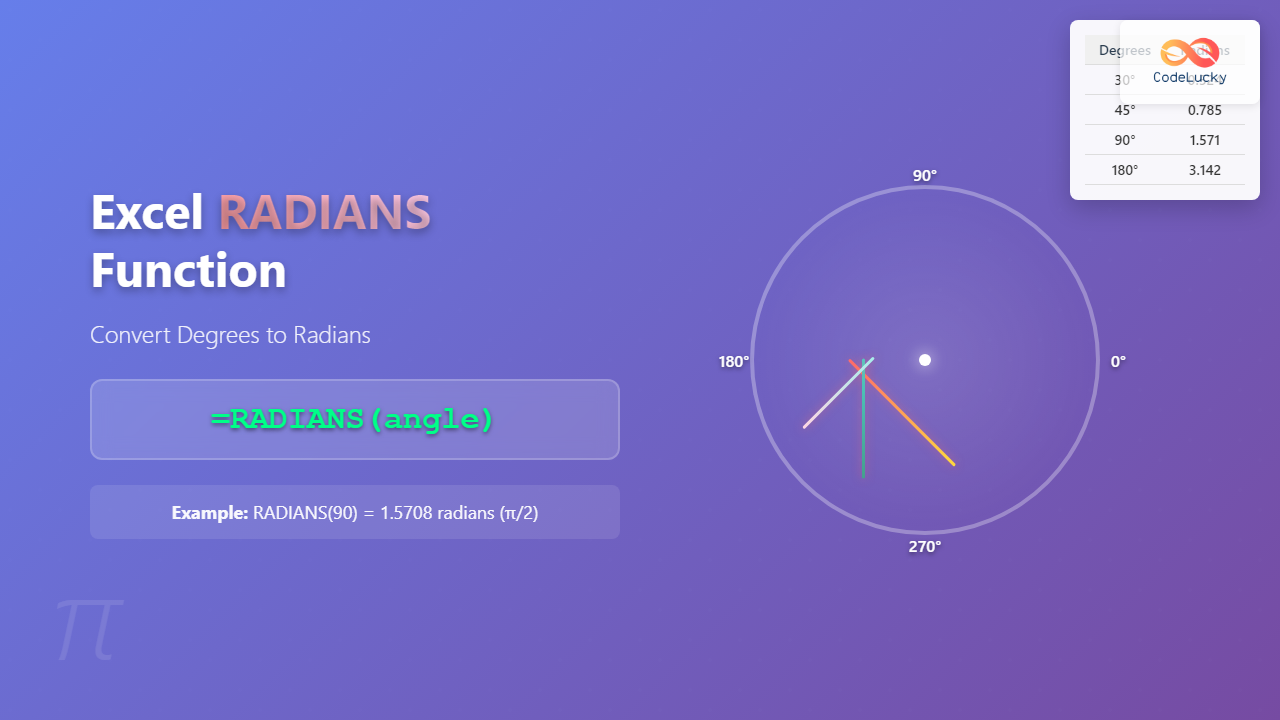
=RADIANS(angle)Parameters
- angle (required): The angle in degrees that you want to convert to radians. This can be a number, cell reference, or formula that returns a numeric value.
Understanding Degrees and Radians
Before diving into practical applications, it’s important to understand the relationship between degrees and radians:
- Degrees: A complete circle contains 360 degrees
- Radians: A complete circle contains 2π radians (approximately 6.28318)
- Conversion formula: Radians = Degrees × (π/180)
The RADIANS function essentially applies this conversion formula automatically, making your calculations more efficient and accurate.
Basic Examples of RADIANS Function
Example 1: Converting Common Angles
| Formula | Result | Description |
|---|---|---|
| =RADIANS(0) | 0 | 0 degrees in radians |
| =RADIANS(30) | 0.523599 | 30 degrees in radians |
| =RADIANS(45) | 0.785398 | 45 degrees in radians |
| =RADIANS(90) | 1.570796 | 90 degrees in radians (π/2) |
| =RADIANS(180) | 3.141593 | 180 degrees in radians (π) |
| =RADIANS(360) | 6.283185 | 360 degrees in radians (2π) |
Example 2: Using Cell References
If you have degree values in column A, you can convert them to radians in column B:
A1: 45
B1: =RADIANS(A1)
Result: 0.785398Advanced Applications and Use Cases
Trigonometric Calculations
The RADIANS function is essential when working with Excel’s trigonometric functions, which expect angles in radians:
=SIN(RADIANS(30)) ' Returns 0.5
=COS(RADIANS(60)) ' Returns 0.5
=TAN(RADIANS(45)) ' Returns 1Engineering Applications
In engineering calculations, you might need to convert bearing angles or rotational measurements:
=RADIANS(B2) ' Where B2 contains bearing in degreesPhysics Calculations
For physics formulas involving angular velocity or wave calculations:
=2*PI()*frequency*RADIANS(phase_angle)Combining RADIANS with Other Functions
With Trigonometric Functions
=SIN(RADIANS(A1))*radius ' Calculate y-coordinate on a circle
=COS(RADIANS(A1))*radius ' Calculate x-coordinate on a circleWith Mathematical Operations
=RADIANS(A1+B1) ' Convert sum of angles
=RADIANS(ABS(A1)) ' Convert absolute value of angleError Handling and Troubleshooting
Common Errors
- #VALUE! Error: Occurs when the input is not a numeric value
- #NAME? Error: Happens when the function name is misspelled
Best Practices
- Always ensure input values are numeric
- Use cell references for dynamic calculations
- Consider using ISNUMBER() function to validate inputs
- Round results when necessary for cleaner presentation
Practical Examples and Templates
Example 1: Angle Conversion Table
Create a comprehensive conversion table:
| Degrees | Formula | Radians | Radians (π) |
|---|---|---|---|
| 0 | =RADIANS(0) | 0 | 0 |
| 30 | =RADIANS(30) | 0.524 | π/6 |
| 45 | =RADIANS(45) | 0.785 | π/4 |
| 60 | =RADIANS(60) | 1.047 | π/3 |
| 90 | =RADIANS(90) | 1.571 | π/2 |
Example 2: Circular Motion Calculator
Calculate position coordinates for circular motion:
X-coordinate: =radius*COS(RADIANS(angle))
Y-coordinate: =radius*SIN(RADIANS(angle))Performance Tips and Optimization
- Avoid nested functions when possible for better performance
- Use absolute references ($A$1) when copying formulas
- Consider array formulas for bulk conversions
- Cache results if the same angles are used repeatedly
Alternative Methods
Manual Calculation
You can also convert degrees to radians manually using:
=A1*PI()/180However, using the RADIANS function is more readable and less prone to errors.
VBA Implementation
For advanced users, you can create custom VBA functions:
Function DegreesToRadians(degrees As Double) As Double
DegreesToRadians = degrees * Application.WorksheetFunction.Pi / 180
End FunctionReal-World Applications
Navigation and GPS
Converting compass bearings for distance calculations:
=RADIANS(bearing_degrees) ' For use in distance formulasArchitecture and Construction
Converting roof angles or structural angles:
=TAN(RADIANS(roof_angle))*horizontal_distance ' Calculate riseScientific Research
For wave analysis, pendulum calculations, and rotational mechanics:
=amplitude*SIN(RADIANS(phase_angle)) ' Wave calculationsVersion Compatibility
The RADIANS function is available in:
- Microsoft Excel 2007 and later versions
- Excel for Microsoft 365
- Excel Online
- Excel for Mac
- Google Sheets (as an alternative)
Conclusion
The Excel RADIANS function is an indispensable tool for anyone working with trigonometric calculations, engineering applications, or mathematical modeling. Its simple syntax and reliable performance make it the preferred method for converting degrees to radians in Excel spreadsheets.
By mastering this function and understanding its applications, you can enhance your Excel skills and tackle more complex mathematical problems with confidence. Whether you’re calculating coordinates, analyzing wave patterns, or working with rotational data, the RADIANS function provides the accuracy and efficiency you need.
Remember to combine it with other trigonometric functions for maximum effectiveness, and always validate your inputs to ensure accurate results. With practice, you’ll find that the RADIANS function becomes an essential part of your Excel toolkit for mathematical and scientific calculations.
- What is the Excel RADIANS Function?
- RADIANS Function Syntax
- Understanding Degrees and Radians
- Basic Examples of RADIANS Function
- Advanced Applications and Use Cases
- Combining RADIANS with Other Functions
- Error Handling and Troubleshooting
- Practical Examples and Templates
- Performance Tips and Optimization
- Alternative Methods
- Real-World Applications
- Version Compatibility
- Conclusion