Depth-First Search (DFS) is one of the most fundamental algorithms in computer science for systematically exploring trees and graphs. It is widely used in search problems, connectivity analysis, cycle detection, topological sorting, solving puzzles (like mazes or Sudoku), and AI pathfinding. Unlike Breadth-First Search (BFS) which explores level by level, DFS dives deeper into one branch before backtracking, thus mimicking a human exploring paths in depth-first fashion.
What is Depth-First Search (DFS)?
DFS is a graph traversal algorithm that starts from a given node (or root in a tree) and explores as far as possible along one branch. When no further nodes are available, it backtracks to continue exploring other unexplored branches. Its recursive nature makes it elegant and easy to implement.
Key Properties of DFS
- Traversal Approach: Depth-oriented, follows a path until it cannot go further.
- Implementation: Can be implemented recursively or using an explicit stack.
- Time Complexity: O(V + E), where V = number of vertices, E = number of edges.
- Space Complexity: Depends on recursion depth; worst-case O(V).
- Applications: Pathfinding, cycle detection, connected components, solving puzzles, detecting bridges and articulation points.
How DFS Works?
DFS follows these steps:
- Start from a node (source or root).
- Visit the node and mark it as visited.
- Recursively visit all unvisited neighbors.
- Backtrack when no further unvisited neighbors are present.
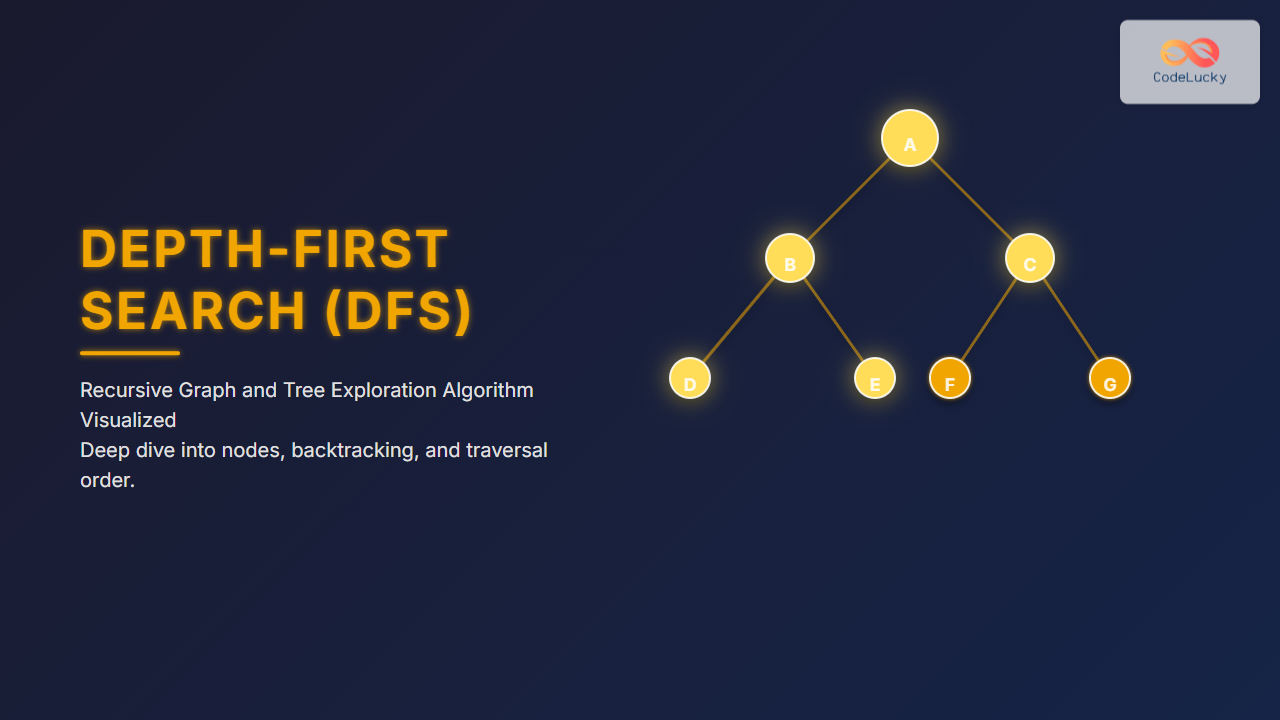
DFS Traversal on a Graph Example
Consider the following graph structure:
If we start DFS from node A, the traversal order could be: A → B → D → E → C → F → G.
Recursive DFS in Python
def dfs_recursive(graph, node, visited=None):
if visited is None:
visited = set()
visited.add(node)
print(node, end=" ")
for neighbor in graph[node]:
if neighbor not in visited:
dfs_recursive(graph, neighbor, visited)
# Example usage:
graph = {
'A': ['B', 'C'],
'B': ['D', 'E'],
'C': ['F', 'G'],
'D': [],
'E': [],
'F': [],
'G': []
}
dfs_recursive(graph, 'A')
Output:
A B D E C F G
DFS on a Tree Example
DFS is particularly simple on trees since there are no cycles.
DFS Preorder Traversal (Root → Left → Right): A → B → D → E → C → F
class Node:
def __init__(self, value):
self.value = value
self.left = None
self.right = None
def dfs_tree(root):
if root:
print(root.value, end=" ")
dfs_tree(root.left)
dfs_tree(root.right)
# Example tree
root = Node('A')
root.left = Node('B')
root.right = Node('C')
root.left.left = Node('D')
root.left.right = Node('E')
root.right.left = Node('F')
dfs_tree(root)
Output:
A B D E C F
DFS vs BFS
DFS and BFS are two primary graph traversal algorithms. The key differences:
| Aspect | DFS | BFS |
|---|---|---|
| Traversal | Depth-first (go deep before backtracking) | Breadth-first (level order) |
| Data Structure | Recursive stack or manual stack | Queue |
| Use Cases | Cycle detection, pathfinding, recursive problems | Shortest path in unweighted graphs, level-order traversal |
Applications of Depth-First Search
- Cycle Detection: Identify if a graph contains cycles.
- Pathfinding: Used in AI and puzzle-solving like maze navigation.
- Connected Components: Find all connected nodes in graphs.
- Topological Sorting: Crucial in dependency resolution.
- Solving Backtracking Problems: Sudoku, N-Queens, and other search-based puzzles.
Interactive DFS Visualization (Python Example)
Here’s a simple interactive example where we track entry and exit of nodes:
def dfs_interactive(graph, node, visited=None, depth=0):
if visited is None:
visited = set()
visited.add(node)
print(" " * depth + f"Entering {node}")
for neighbor in graph[node]:
if neighbor not in visited:
dfs_interactive(graph, neighbor, visited, depth + 2)
print(" " * depth + f"Exiting {node}")
graph = {
'A': ['B', 'C'],
'B': ['D', 'E'],
'C': ['F'],
'D': [],
'E': [],
'F': []
}
dfs_interactive(graph, 'A')
Sample Output:
Entering A
Entering B
Entering D
Exiting D
Entering E
Exiting E
Exiting B
Entering C
Entering F
Exiting F
Exiting C
Exiting A
Conclusion
Depth-First Search (DFS) is an elegant and powerful algorithm that plays a central role in computer science. Its recursive nature makes it simple to implement and useful for numerous applications like pathfinding, cycle detection, and solving backtracking problems. By understanding DFS on both trees and graphs, you can build a strong foundation for tackling advanced algorithms and real-world computational challenges.