Cuckoo Hashing: Guaranteed O(1) Worst-Case Lookup for Efficient Data Access

Cuckoo Hashing is an advanced hashing technique designed to guarantee O(1) worst-case lookup time in hash tables, overcoming collisions efficiently through a clever eviction method. This article dives deep into how cuckoo hashing achieves this guarantee, providing detailed insights, illustrative examples, and visualizations to help you master this powerful algorithm.

Table of Contents

What is Cuckoo Hashing?

Cuckoo Hashing is a collision resolution strategy for hash tables that uses two (or more) hash functions and two separate tables (or one table split logically). When inserting a key, it has two possible locations based on the two hash functions. If one location is occupied, the existing key is “kicked out” (evicted) and moved to its alternative location, potentially causing a chain of evictions until all keys fit without collision.

This approach ensures constant-time lookups in the worst case by keeping each key in one of only two possible places, avoiding long chains or probing sequences.

Why Use Cuckoo Hashing?

Guaranteed O(1) Lookups: Unlike traditional chaining or linear probing, cuckoo hashing guarantees constant time lookups without degradation.
Simple and Fast Lookups: Only two possible slots to check, which is faster than probing multiple locations or traversing linked lists.
Cache Efficient: Constant lookups mean predictable memory access patterns, benefiting modern CPU cache behavior.

Core Components of Cuckoo Hashing

The key elements of cuckoo hashing are:

Two hash functions: \( h_1(k) \) and \( h_2(k) \) that map each key \( k \) to two possible positions in the hash table.
Two hash tables (or one with two logical segments): Positions correspond to indices via the two hash functions.
Eviction mechanism: If both candidate slots are occupied during insertion, the existing key is displaced and reinserted using its alternate hash position.

Detailed Insertion Algorithm

To insert a key \(k\):

Check position \(h_1(k)\) in the first table. If empty, insert key there.
If \(h_1(k)\) is occupied, check \(h_2(k)\) in the second table. If empty, insert key there.
If both positions are occupied, evict the current occupant of \(h_1(k)\), place \(k\) there, then reinsert the evicted key using its alternative hash function.
This may cause a chain of evictions, which continues up to a fixed threshold (like a maximum number of displacements). If limit is exceeded, the table is rebuilt with new hash functions.

Example of Cuckoo Hashing

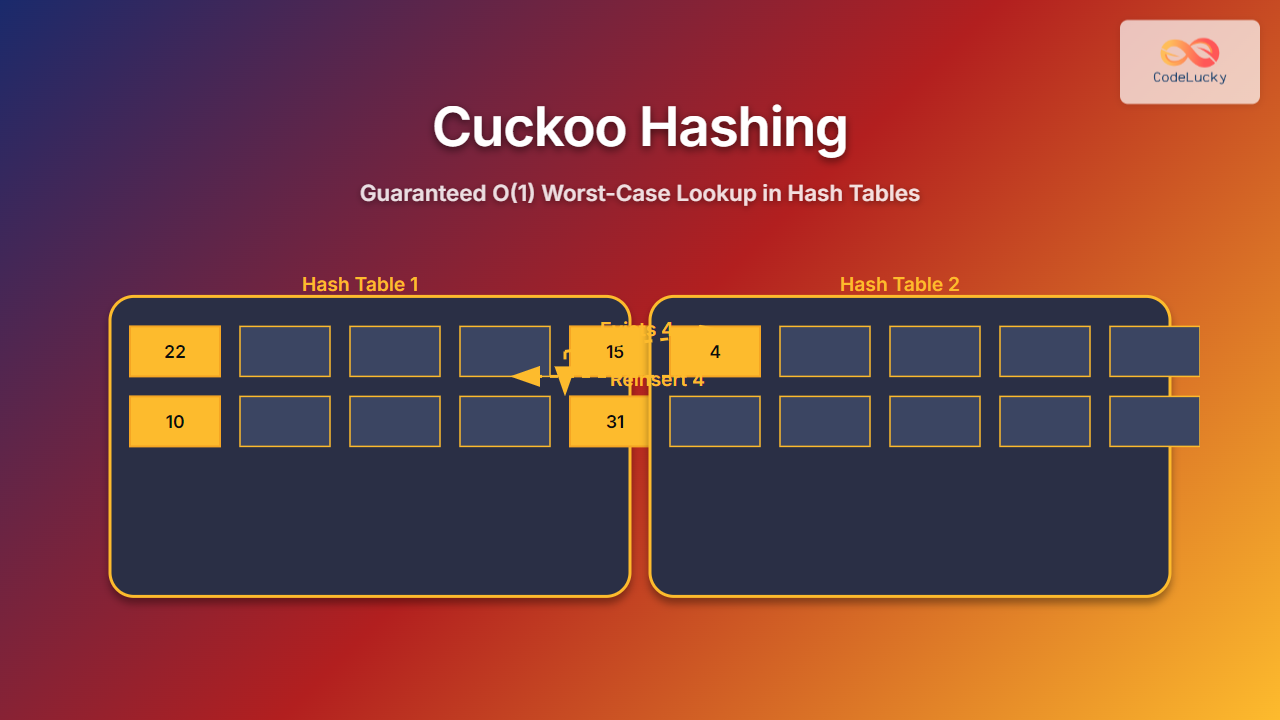
Consider inserting keys 10, 22, 31, 4, 15 into a cuckoo hash table with two hash functions:

\(h_1(k) = k \mod 11\)
\(h_2(k) = \lfloor k/11 \rfloor \mod 11\)

Insert 10: \(h_1(10) = 10\), slot empty, insert there.

Insert 22: \(h_1(22) = 0\), slot empty, insert there.

Insert 31: \(h_1(31) = 9\), slot empty, insert there.

Insert 4: \(h_1(4) = 4\), slot empty, insert there.

Insert 15: \(h_1(15) = 4\) but slot occupied by 4. Evict 4, insert 15 at slot 4; now reinsert 4 using \(h_2(4) = \lfloor4/11\rfloor \mod 11 = 0\), slot 0 occupied by 22, so evict 22 and put 4 there. Reinsert 22 at \(h_2(22) = \lfloor22/11\rfloor \mod 11 = 2\), slot 2 empty, insert 22 there.

Lookup Operation

To search for a key \(k\), check positions \(h_1(k)\) and \(h_2(k)\). If key is found in either, return successful. Otherwise, key is absent.

This requires exactly two memory lookups in the worst case, guaranteeing O(1) worst-case lookup time.

Deletion Operation

Deletion is straightforward—check both positions, if found, remove the key.

Handling Cycles and Rehashing

Because key insertion can cause chains of evictions, it is possible to get into cycles where keys are shuffled infinitely. To manage this, cuckoo hashing implementations typically:

Set a maximum number of displacement attempts per insertion.
If exceeded, perform a rehashing with new hash functions and possibly a larger table size.

Advantages and Limitations

Advantages	Limitations
Guaranteed O(1) Lookup: Most notable benefit Simpler than chained hashing in access pattern Memory overhead is low compared to chaining	Insertions can be costly due to multiple evictions Cycle detection and rehashing add complexity Requires good hash functions for performance

Interactive Example: Visualizing Cuckoo Insertion

Here is a simple textual illustration of how cuckoo hashing displaces keys on collision. Suppose you want to insert 15 and it collides as in the example above:


Initial Table1: [22, -, -, -, 4, -, -, -, -, 31, 10]
Table2:        [-, -, -, -, -, -, -, -, -, -, -]

Insert(15):
  1. h1(15) = 4 occupied by 4, evict 4
  2. Place 15 at position 4 in Table1
  3. Reinsert 4 using h2(4) = 0 in Table2 empty, place 4 there
Result:
Table1: [22, -, -, -, 15, -, -, -, -, 31, 10]
Table2: [4, -, -, -, -, -, -, -, -, -, -]

Conclusion

Cuckoo hashing is a compelling alternative to traditional hash tables that ensures worst-case constant-time lookups through a combination of multiple hash functions and a smart eviction strategy. Though insertions can involve multiple displacements and occasional rehashing, the trade-off results in extremely efficient and predictable lookups, making cuckoo hashing ideal for performance-critical applications like networking, databases, and real-time systems.

Understanding cuckoo hashing thoroughly, including its eviction and rehashing mechanisms, helps developers design optimized data structures and algorithms with guaranteed performance bounds for hash-based operations.