Counting Sort Algorithm: Non-Comparison Integer Sorting with Examples

Sorting algorithms form the backbone of computer science fundamentals, aiding efficient data organization and retrieval. Most traditional sorting algorithms like QuickSort and MergeSort rely on comparisons. However, Counting Sort is different—it is a non-comparison-based algorithm suitable for sorting integers within a specific range. This makes it extremely efficient for scenarios where the range of numbers is not significantly larger than the number of elements.

Table of Contents

What is Counting Sort?

Counting Sort is an integer sorting technique that works by counting the number of occurrences of each unique value in the input array. These counts are then used to determine the position of each element in the output array. Unlike comparison-based algorithms, Counting Sort achieves linear time complexity under suitable constraints.

Key Characteristics:

Non-comparative: It does not compare elements to sort them.
Stable: Equal values preserve their input order in the sorted output.
Efficient: Optimal when input contains integers within a known, limited range.

How Counting Sort Works (Step-by-Step)

Let’s understand Counting Sort with an example input array:

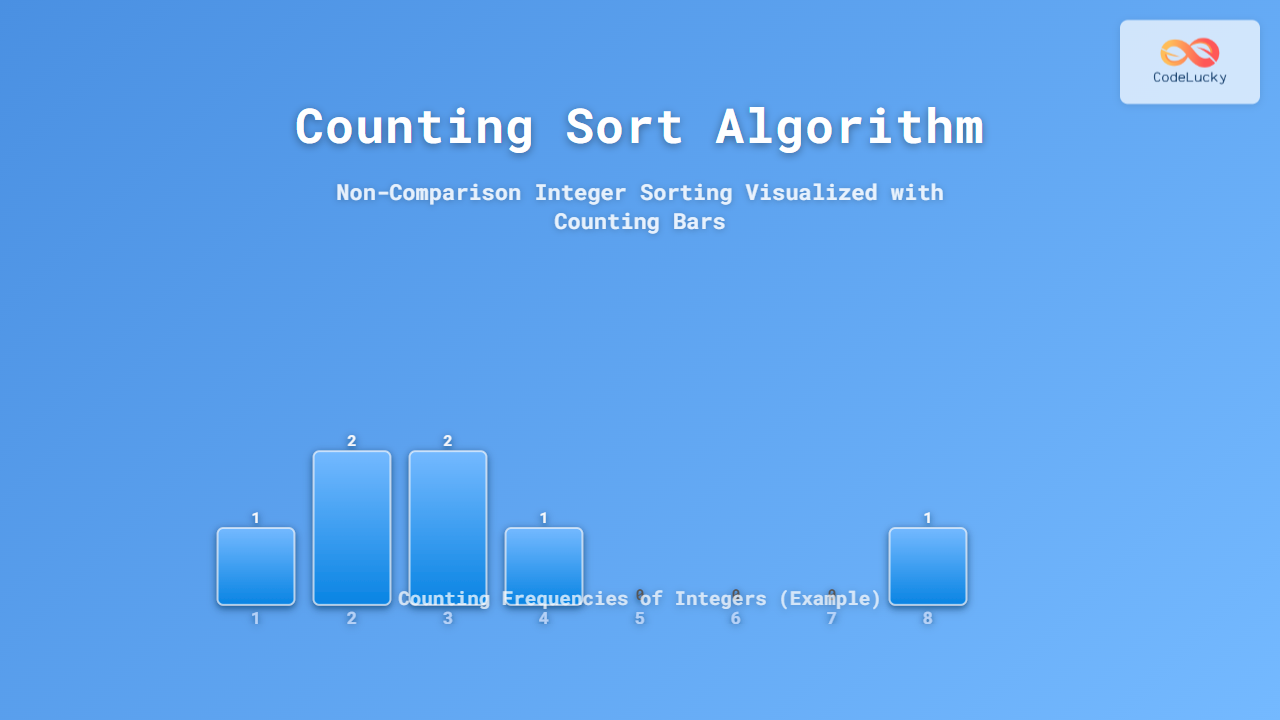
Input: [4, 2, 2, 8, 3, 3, 1]

Find the range: Minimum = 1, Maximum = 8.
Initialize count array: An array of size max - min + 1 filled with zeros.
Store frequency: Count the occurrences of each integer.
Cumulative count: Modify the count array to hold positions of elements.
Build output: Traverse the input array backward (for stability), placing each element in its correct output position.

Here is a visualization:

Example with Step Output

Input: [4, 2, 2, 8, 3, 3, 1]

Step 1: Count occurrences
Count Array: [0,1,2,2,1,0,0,1]  (Index = number, Value = frequency)

Step 2: Cumulative count
Count Array: [0,1,3,5,6,6,6,7]

Step 3: Place into output
Output: [1, 2, 2, 3, 3, 4, 8]

Python Implementation of Counting Sort


def counting_sort(arr):
    if not arr:
        return arr  # Handle empty input
    
    # Find min and max value
    min_val, max_val = min(arr), max(arr)
    
    # Initialize count array
    count = [0] * (max_val - min_val + 1)
    
    # Count frequencies
    for num in arr:
        count[num - min_val] += 1
    
    # Cumulative count
    for i in range(1, len(count)):
        count[i] += count[i-1]
    
    # Build output array (stable sorting: iterate backwards)
    output = [0] * len(arr)
    for num in reversed(arr):
        count[num - min_val] -= 1
        new_position = count[num - min_val]
        output[new_position] = num
    
    return output

# Example
arr = [4, 2, 2, 8, 3, 3, 1]
print("Sorted Array:", counting_sort(arr))

Output:

Sorted Array: [1, 2, 2, 3, 3, 4, 8]

Time and Space Complexity

Time Complexity: O(n + k), where n is number of elements, k is range (max – min + 1).
Space Complexity: O(n + k), since we require an auxiliary array for counts and output.
Stability: Yes, when built properly by inserting elements from right to left.

When to Use Counting Sort?

Counting Sort is particularly useful when:

The input contains only integers (or small range discrete values).
The maximum and minimum values are not extremely far apart.
Stability of sorting is required (for sorting by multiple fields).

It is not recommended when the range of numbers (k) is significantly larger than the number of elements (n), as it makes memory usage impractical.

Interactive Example (Dry Run)

Let’s try manually running for input [5, 1, 4, 2]:

Count Occurrences: [1,1,1,0,1] (for numbers 1 to 5)
Cumulative Count: [1,2,3,3,4]
Output Construction:
  - Place 2 at position 1
  - Place 4 at position 2
  - Place 1 at position 0
  - Place 5 at position 3

Result = [1, 2, 4, 5]

Conclusion

The Counting Sort Algorithm is a powerful tool when dealing with integer-based datasets that fall within a constrained range. Its linear-time performance, stability, and simplicity make it a preferred choice in specialized circumstances. However, practical implementation demands an understanding of its space trade-offs. When applied correctly, Counting Sort consistently delivers optimal sorting efficiency.