In computer science, hashing is a critical technique used to achieve quick data retrieval. However, when two keys hash to the same index, collision occurs. This article explores two popular collision resolution techniques in hash tables: Chaining and Open Addressing. Understanding these techniques helps developers design efficient hash tables with minimal performance degradation.
What is Collision in Hashing?
A hash table uses a hash function to compute an index for storing data. When two or more keys map to the same index, it leads to a collision. Handling collisions efficiently is vital since uncontrolled collisions degrade the constant time complexity (O(1)) of hash table operations.
Collision Resolution Techniques Overview
There are two main strategies to resolve collisions:
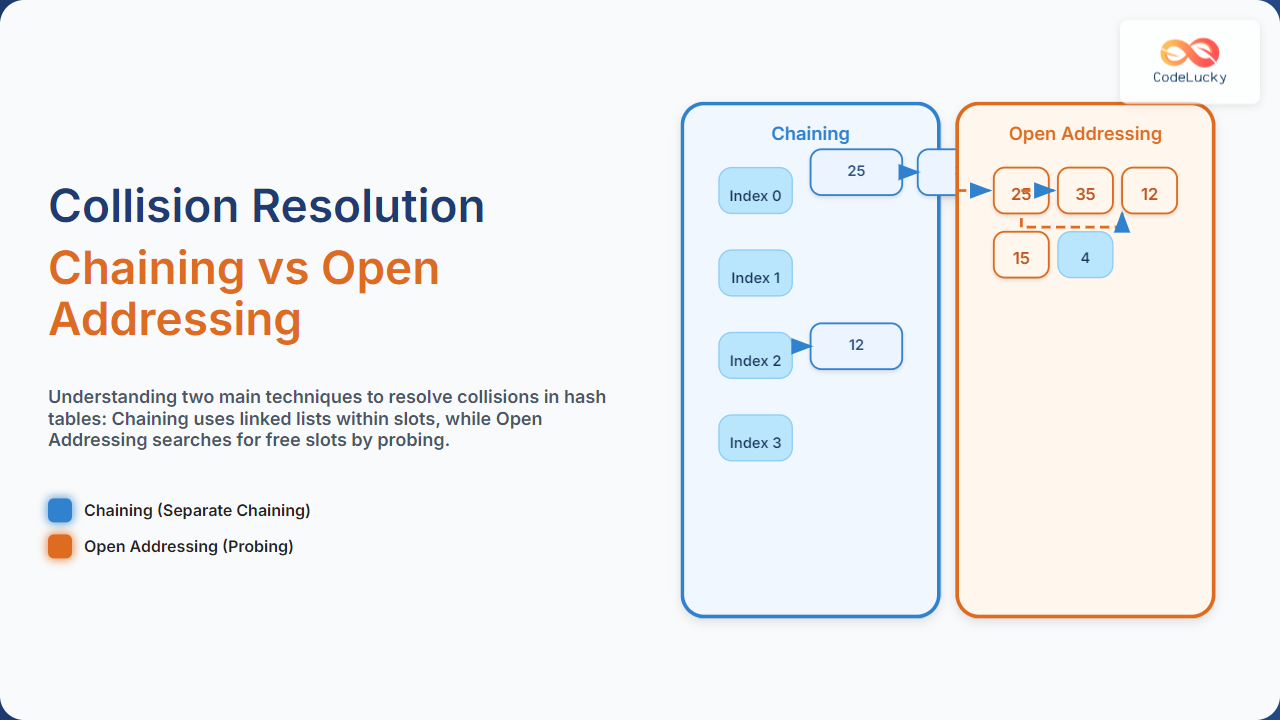
- Chaining (Separate Chaining): Each slot contains a linked list (or another data structure) of all elements hashing to that index.
- Open Addressing (Closed Hashing): Upon collision, probe to find another empty slot in the hash table itself using systematic searching.
Chaining (Separate Chaining) Explained
In chaining, each hash table slot points to a linked list of entries that share the same hash index. When a collision occurs, the new element is appended to the list at that slot.
This method allows multiple elements to exist at the same index but requires additional memory to store pointers for the linked list.
Example of Chaining
Hash Table size = 5
Keys to insert: 12, 25, 35, 15
Hash function: key % 5
Inserting keys:
12 % 5 = 2 → insert 12 at index 2
25 % 5 = 0 → insert 25 at index 0
35 % 5 = 0 → collision! Append 35 to linked list at index 0
15 % 5 = 0 → collision! Append 15 as well at index 0
Result:
Index 0: 25 → 35 → 15 (linked list)
Index 2: 12
Other indices are empty
Open Addressing Explained
Open Addressing stores all elements directly within the hash table array. When a collision occurs, it searches the table for the next available slot using a probing sequence.
Common probing methods include:
- Linear Probing: Check subsequent slots one by one until an empty slot is found.
- Quadratic Probing: Use quadratic function offsets from the original hash to find a free slot.
- Double Hashing: Use a second hash function to calculate step size for searching empty slots.
Example of Open Addressing with Linear Probing
Hash Table size = 5
Keys to insert: 12, 25, 35, 15
Hash function: key % 5
Inserting keys:
12 % 5 = 2 → insert 12 at index 2
25 % 5 = 0 → insert 25 at index 0
35 % 5 = 0 → collision! Check index 1 → empty, insert 35 there
15 % 5 = 0 → collision! index 0 full, index 1 full, check index 2 full, check index 3 → empty, insert 15 there
Resulting table:
Index 0: 25
Index 1: 35
Index 2: 12
Index 3: 15
Index 4: Empty
Comparing Chaining and Open Addressing
| Feature | Chaining | Open Addressing |
|---|---|---|
| Storage | Uses extra memory for linked lists or chains | Stores all elements inside the hash table array |
| Collision Handling | Stores collided elements in a linked list per bucket | Finds alternate empty slots using probing sequences |
| Performance | Performance depends on linked list length, can degrade if many collisions | Performance depends on load factor and probing strategy |
| Deletion | Easy to delete nodes from linked lists | More complex; needs special markers to avoid search disruption |
| Table Load | Can handle load factors above 1 safely | Performance suffers when load factor approaches 1; ideally kept under 0.7 |
When to Use Which?
Chaining is preferred when the hash table may have a high load factor or unknown data quantity, as it gracefully handles many collisions. It also simplifies deletion.
Open Addressing saves memory by avoiding extra pointers and can be faster with low load factors and good hash functions. However, it requires careful management of deletion and load factors to avoid clustering issues.
Visual Summary Diagram
Conclusion
Understanding and choosing the right collision resolution technique is essential for designing efficient hash tables. Chaining offers flexibility and ease of use with some additional memory cost. In contrast, Open Addressing uses array space more efficiently but requires more careful handling of operations like deletion and proper load management. Both have their places in algorithms depending on use case and performance requirements.