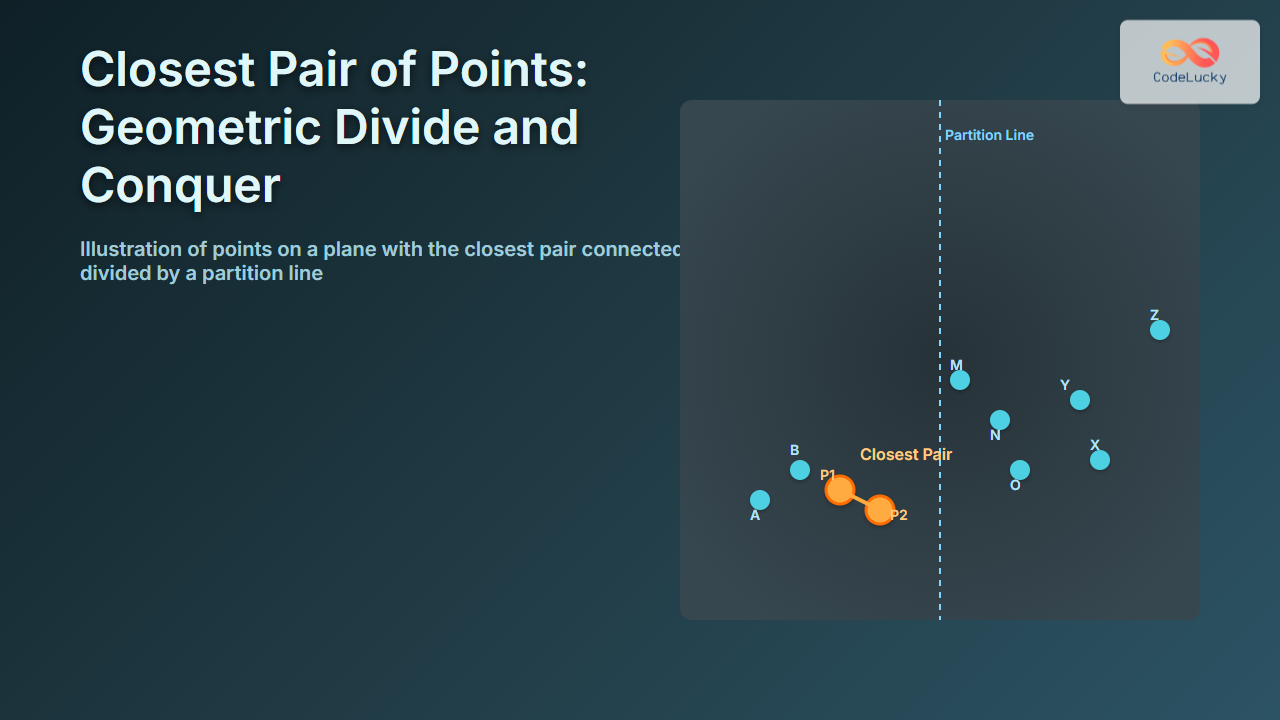
The Closest Pair of Points problem is a fundamental algorithmic challenge in computational geometry—finding the two closest points among a set of given points in a two-dimensional plane. This problem has significant applications in computer graphics, pattern recognition, geographic information systems, and more.
This article dives deep into the geometric divide and conquer approach to solve the closest pair problem efficiently, explaining the algorithm’s intuition, implementation details, and optimizations with illustrative examples, visualizations, and clear code snippets. By the end, readers will have a practical, solid understanding of this essential geometric algorithm.
Understanding the Problem
Given n points in a plane, the goal is to identify the pair of points with the smallest Euclidean distance between them.
Naively, a brute-force approach compares each point to every other point, leading to an O(n²) runtime, which is inefficient for large datasets.
Using divide and conquer, we can improve the runtime to O(n log n), making it much more practical.
Key Idea of the Divide and Conquer Approach
The algorithm follows these main steps:
- Sort the points by their X-coordinate.
- Divide the point set into two equal halves.
- Recursively find the closest pair in each half (left and right).
- Combine: Find the closest pair that crosses the partition line.
Step-by-Step Explanation
1. Sorting Points by X-Coordinate
Sort the points initially so that dividing them into halves is straightforward and logical.
2. Recursive Divide
Recursively split the points until a base case is reached: when the subset size is small (normally 2 or 3 points), solve by brute force.
3. Conquer by Combining Results
After recursively finding the closest pairs on both halves, the minimum distance d between these pairs is noted.
4. Checking Points near the Middle Strip
The crucial part is checking pairs where one point lies in the left half and the other in the right half, but the points must be d units close to the middle dividing line.
We build a strip of points within distance d from the center line, sorted by Y-coordinate.
Each point in this strip needs to be compared only to the next up to 7 points in the strip to identify any closer pairs (based on geometric properties).
Example Walkthrough
Consider this set of points:
Points = [(2, 3), (12, 30), (40, 50), (5, 1), (12, 10), (3, 4)]
Steps:
- Sort by X: [(2,3), (3,4), (5,1), (12,10), (12,30), (40,50)]
- Divide into halves:
- Left: [(2,3), (3,4), (5,1)]
- Right: [(12,10), (12,30), (40,50)]
- Recursively find closest pairs in each half:
- Left closest: distance between (2,3) & (3,4) = 1.414
- Right closest: distance between (12,10) & (12,30) = 20
- Minimum distance between halves: 1.414
- Check points in the strip around midline (X ~ 8.5)
- Points within 1.414 of midline: (5,1), (12,10)
- Distance between these points > 1.414, so no update.
- Closest pair overall: (2,3) and (3,4)
Python Code Example
def dist(p1, p2):
return ((p1[0]-p2[0])**2 + (p1[1]-p2[1])**2)**0.5
def brute_force(points):
min_dist = float('inf')
pair = None
for i in range(len(points)):
for j in range(i+1, len(points)):
d = dist(points[i], points[j])
if d < min_dist:
min_dist = d
pair = (points[i], points[j])
return min_dist, pair
def strip_closest(strip, d):
min_dist = d
pair = None
strip.sort(key=lambda x: x[1]) # sort by Y coordinate
for i in range(len(strip)):
j = i + 1
while j < len(strip) and (strip[j][1] - strip[i][1]) < min_dist:
dist_curr = dist(strip[i], strip[j])
if dist_curr < min_dist:
min_dist = dist_curr
pair = (strip[i], strip[j])
j += 1
return min_dist, pair
def closest_pair_rec(points):
if len(points) <= 3:
return brute_force(points)
mid = len(points)//2
mid_point = points[mid]
dl, pair_left = closest_pair_rec(points[:mid])
dr, pair_right = closest_pair_rec(points[mid:])
d = min(dl, dr)
pair = pair_left if dl <= dr else pair_right
strip = [p for p in points if abs(p[0] - mid_point[0]) < d]
ds, pair_strip = strip_closest(strip, d)
if ds < d:
return ds, pair_strip
return d, pair
def closest_pair(points):
sorted_points = sorted(points, key=lambda x: x[0])
distance, pair = closest_pair_rec(sorted_points)
return distance, pair
points = [(2,3), (12,30), (40,50), (5,1), (12,10), (3,4)]
print(closest_pair(points))
This code elegantly demonstrates the divide and conquer steps while preserving efficiency.
Why Only Check Next 7 Points in the Strip?
Geometric proof shows that in the strip area, each point only needs to be checked against the next up to 7 points in Y-sorted order. This drastically lowers comparisons in this step and is the reason the algorithm runs in O(n log n) time. The underlying theory leverages packing arguments in the two-dimensional space around the partition.
Summary
The Closest Pair of Points problem solved via geometric divide and conquer is a classic example of how careful algorithm design reduces a brute-force quadratic runtime to a much faster O(n log n) performance.
This method combines sorting, recursion, and subtle geometric insights to effectively reduce the search space and comparisons.
Understanding this algorithm imparts crucial skills in algorithmic thinking, geometric data structure design, and optimization patterns applicable in many areas of computer science.
Readers are encouraged to implement this algorithm, experiment with different point sets, and visualize the recursion and strip checking step-by-step for deeper insight.