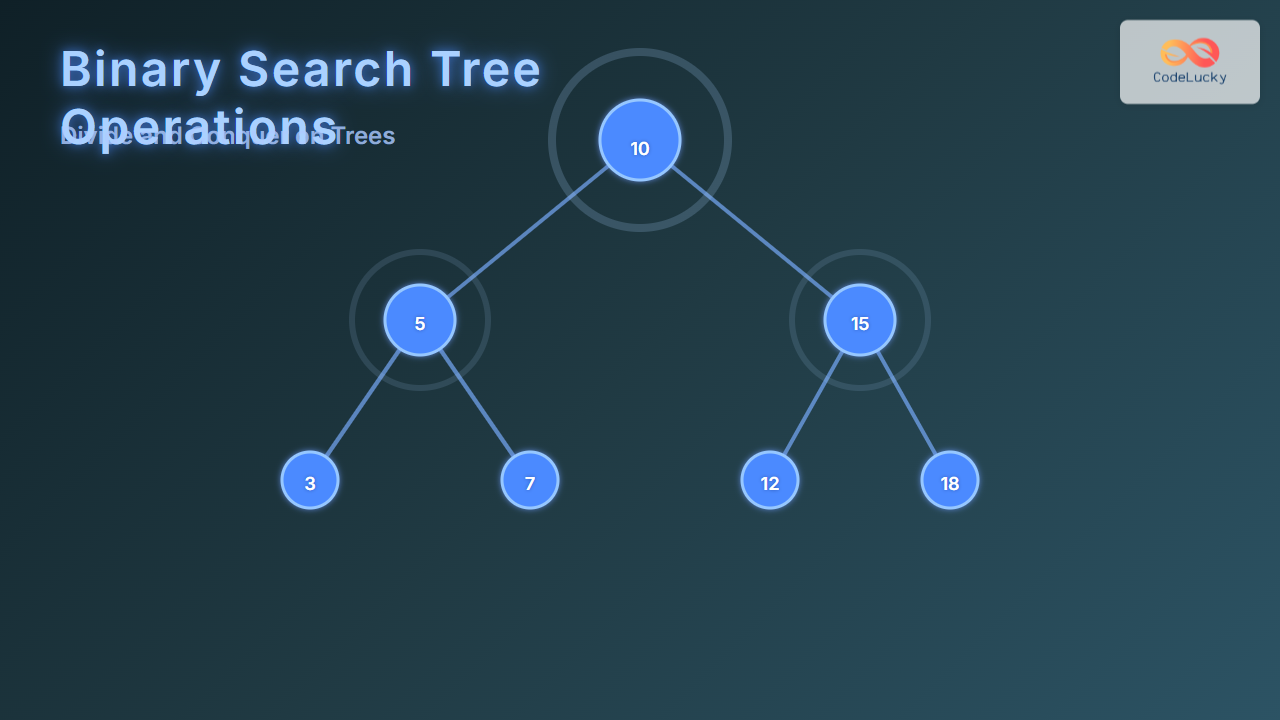
Binary Search Trees (BSTs) stand as a fundamental data structure in computer science, enabling efficient data storage, retrieval, and manipulation. Leveraging the divide and conquer strategy in BST operations forms the core of many classic algorithms applied on trees. This article explores detailed BST operations, illustrating how divide and conquer manifests elegantly in trees through recursive methodologies, accompanied by step-by-step examples and clear visualizations.
Understanding Binary Search Trees (BSTs)
A Binary Search Tree is a binary tree where each node contains a key, and the keys in the left subtree are less than the node’s key while those in the right subtree are greater. This property enables rapid searching, insertion, and deletion operations.
This diagram shows a sample BST where each subtree respects the BST property, essential for divide and conquer recursion.
Divide and Conquer Strategy in BST Operations
The divide and conquer approach breaks down a large problem into smaller subproblems, solves each subproblem recursively, and combines their solutions. BSTs naturally fit this approach because each operation focuses on subtrees defined by the current node.
- Divide: Consider the current node and split the problem into left and right subtree.
- Conquer: Recursively solve the operation on left and/or right subtree.
- Combine: Process the current node’s data possibly combining subtree results.
1. Searching in a BST Using Divide and Conquer
To search for a value in a BST:
- Compare it with the current node’s value.
- If equal, return the node.
- If smaller, recurse into the left subtree.
- If larger, recurse into the right subtree.
def bst_search(node, key):
if node is None or node.key == key:
return node
if key < node.key:
return bst_search(node.left, key)
else:
return bst_search(node.right, key)
Example search for 7 in the BST above:
2. Insertion in a BST
Insertion recursively finds the correct spot for the new key and inserts a new node:
def bst_insert(node, key):
if node is None:
return Node(key)
if key < node.key:
node.left = bst_insert(node.left, key)
else:
node.right = bst_insert(node.right, key)
return node
Example: Inserting 13 into the BST:
3. Deleting a Node in BST (Divide and Conquer)
Deletion has three cases and uses recursion to adjust the tree:
- Leaf node: Remove directly.
- One child: Replace node with child.
- Two children: Find the inorder successor (smallest in right subtree), replace current node’s key, then delete that successor recursively.
def bst_delete(node, key):
if node is None:
return node
if key < node.key:
node.left = bst_delete(node.left, key)
elif key > node.key:
node.right = bst_delete(node.right, key)
else:
# Node to delete found
if node.left is None:
return node.right
if node.right is None:
return node.left
# Two children case
temp = find_min(node.right)
node.key = temp.key
node.right = bst_delete(node.right, temp.key)
return node
def find_min(node):
while node.left:
node = node.left
return node
Deleting 15 in the above example:
4. Traversal Operations Illustrate Divide and Conquer
Traversals process the nodes recursively by breaking down the tree into subtrees and combining results:
| Traversal Type | Recursive Divide and Conquer Explanation | Visit Order Example (for BST above) |
|---|---|---|
| Inorder | Traverse left subtree, visit node, traverse right subtree | 3, 5, 7, 10, 12, 13, 15, 18 |
| Preorder | Visit node, traverse left subtree, traverse right subtree | 10, 5, 3, 7, 15, 12, 13, 18 |
| Postorder | Traverse left subtree, traverse right subtree, visit node | 3, 7, 5, 13, 12, 18, 15, 10 |
5. Interactive Visualization Concept
For a more immersive understanding, an interactive BST viewer can be implemented via frontend frameworks or tools like D3.js, where users can insert, delete, and search visual nodes reflecting divide and conquer recursion live.
Why Divide and Conquer Works Well on Trees
BSTs inherently partition the problem space as each node leads to independent left and right subtrees. This separation enables neatly recursive, efficient operations with a complexity proportional to tree height, typically O(log n) on balanced trees, making divide and conquer a natural paradigm for tree algorithms.
Summary
This detailed exploration shows how fundamental BST operations — searching, insertion, deletion, and traversals — utilize the divide and conquer strategy by recursively partitioning trees into smaller subtrees, solving recursively, and combining results. Practical code snippets and illustrative diagrams help clarify these concepts, making this an essential guide for mastering tree algorithms.