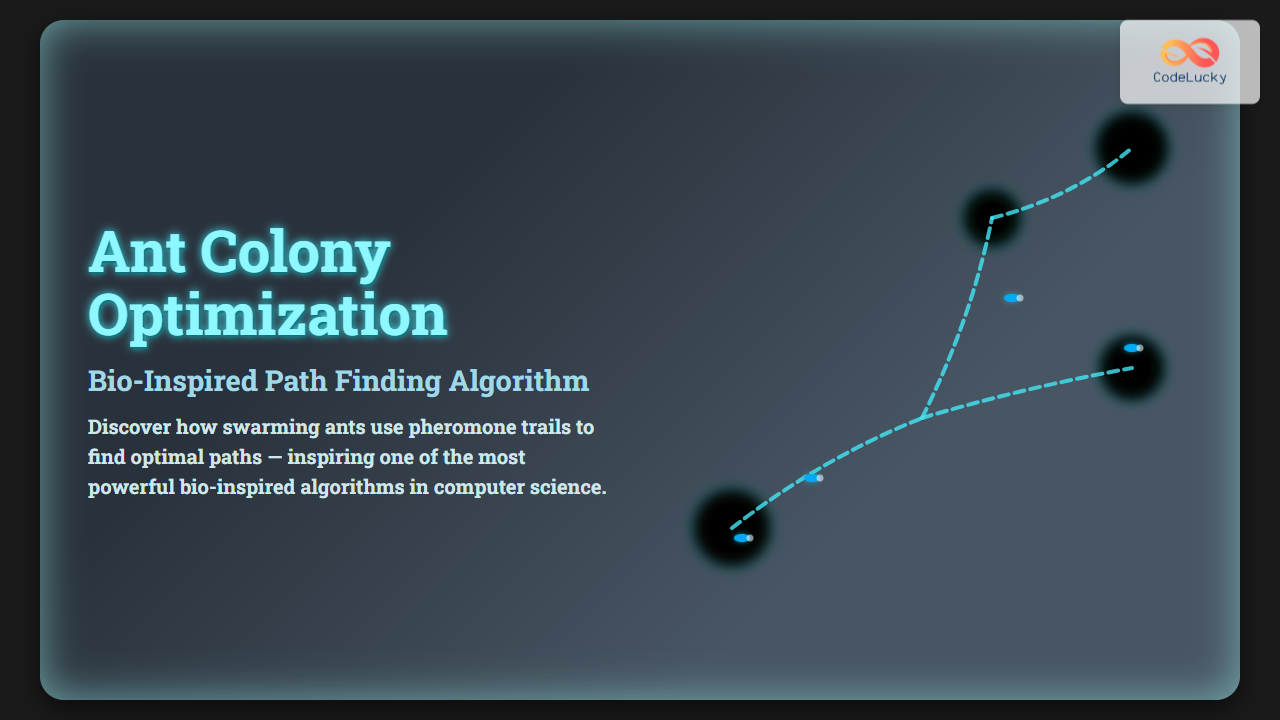
Ant Colony Optimization: Bio-Inspired Path Finding Algorithm Explained

Table of Contents

• Introduction to Ant Colony Optimization (ACO)
• Biological Inspiration: How Real Ants Find Paths
• Mechanics of the ACO Algorithm
• Example: Solving a Path Finding Problem with ACO
• Interactive Visualization of ACO
• Advantages and Limitations
• Real-World Applications
• Conclusion

Introduction to Ant Colony Optimization (ACO)

Ant Colony Optimization is a metaheuristic inspired by the behavior of ants searching for food. It belongs to a class of swarm intelligence algorithms that exploit decentralized, collective problem-solving capabilities.

ACO was primarily designed to tackle combinatorial optimization problems, which involve finding the best ordering or selection among discrete items to optimize a global objective.

Fundamentally, artificial ants stochastically build solutions based on accumulated pheromone trails and problem-specific heuristic information, iteratively reinforcing better paths while allowing exploration of alternatives.

Biological Inspiration: How Real Ants Find Paths

Real ants deposit a chemical substance called pheromone on the ground as they travel. This pheromone acts as a guide for other ants, creating a feedback loop:

• When an ant finds food, it returns to the nest, leaving a pheromone trail.
• Other ants sense this trail and prefer paths with stronger pheromone concentrations.
• Shorter paths get reinforced more quickly because ants traverse them faster, depositing more pheromone per unit time.
• Over time, the colony collectively converges on the shortest path between the nest and food source.

This natural optimization inspires the computational ACO framework. Below is a flow representation of the pheromone-guided path reinforcement in ants:

Mechanics of the ACO Algorithm

The ACO metaheuristic simulates this process with a set of artificial ants that construct candidate solutions to a combinatorial problem over iterations by probabilistically choosing solution components guided by pheromone and heuristics.

Key Components:

• Pheromone Trails: Numerical values associated with solution components representing learned desirability.
• Heuristic Information: Problem-specific knowledge used to bias selection, e.g., inverse of distance in TSP.
• Solution Construction: Ants build solutions incrementally by choosing next components based on pheromone and heuristics.
• Pheromone Update: After solution construction, pheromone trails are updated with evaporation (reducing intensity) and reinforcement (increasing intensity for good solutions).

The probability \(p_{ij}^k\) of ant \(k\) selecting component \(j\) when currently at component \(i\) is typically given by:

Where:

• \(\tau_{ij}\) is pheromone intensity on edge (i,j)
• \(\eta_{ij}\) is heuristic desirability of edge (i,j)
• \(\alpha\) controls pheromone influence
• \(\beta\) controls heuristic influence
• allowed_k is the set of feasible next components for ant \(k\)

The balance of \(\alpha\) and \(\beta\) affects exploitation vs. exploration, crucial for ACO’s performance.

Example: Solving a Path Finding Problem with ACO

Consider a graph representing cities connected by paths with associated distances. The goal is to find the shortest path visiting all nodes (a version of the Traveling Salesman Problem).

Setup:

• Nodes: A, B, C, D
• Distances: A–B: 2, A–C: 9, A–D: 10, B–C: 6, B–D: 4, C–D: 3

Initially, all edges have equal pheromone. Artificial ants start randomly at a node and select the next node probabilistically based on pheromone and inverse distance heuristic.

Over iterations, pheromone updates reinforce shorter routes, and the ants converge towards the shortest Hamiltonian cycle.

This simple graph illustrates how ACO can be applied to path optimization problems by simulating swarm intelligence.

Interactive Visualization of ACO

An interactive simulation can help understand how ants probabilistically choose paths and how pheromone trails evolve:

• Step 1: Initialize pheromones uniformly on all edges.
• Step 2: Each ant builds a path based on a weighted random choice influenced by pheromone and heuristic.
• Step 3: After path construction, update pheromone trails: evaporate a fraction and increase on visited edges proportionally to path quality.
• Step 4: Repeat for multiple iterations until convergence.

While full code and interactive widgets are ideal for web, the key logic for such a simulation in Python can look like this (to embed in a web app or tutorial):

import random

# Pheromone and heuristic matrices here...

for iteration in range(max_iters):
    for ant in ants:
        path = construct_path(pheromone, heuristic)
        length = evaluate_path(path)
        update_pheromones(path, length)

# Visualization can show pheromone intensities as edge thickness or color.

Advantages and Limitations

Advantages:

• Effective for complex combinatorial problems where classical optimization methods struggle.
• Distributed computational model enabling parallelization.
• Flexible framework adaptable to various domains beyond routing.

Limitations:

• Convergence can be slow for very large or dynamic problems.
• Parameter tuning (pheromone influence, evaporation rate) is critical but can be challenging.
• May get trapped in local optima without sufficient exploration strategies.

Real-World Applications

ACO has been successfully applied in:

• Routing: Network routing optimization in telecommunications.
• Logistics: Vehicle routing and supply chain optimization.
• Scheduling: Job-shop and task scheduling problems.
• Robotics: Path planning for autonomous robots.

Conclusion

Ant Colony Optimization offers a fascinating glimpse into how collective behavior and simple agent interactions inspired by nature can solve complex computation problems efficiently. From real ants following pheromone trails to artificial ants exploring solution spaces, the principles of ACO blend biology with computer science for robust optimization frameworks.

Implementing ACO requires a nuanced balance of exploration and exploitation, careful parameter tuning, and problem-specific heuristics—but the rewarding results have made it a cornerstone of bio-inspired algorithms with wide applicability.

For developers and researchers intrigued by swarm intelligence, ACO provides both elegant theory and practical solution strategies worth mastering.