Advanced Data Structure Algorithms: Complex Structure Operations Explained

Advanced data structure algorithms are essential to handling large-scale, complex operations efficiently. While basic structures such as arrays, linked lists, stacks, and queues cover foundational needs, advanced data structures like Segment Trees, B-Trees, Fibonacci Heaps, Disjoint Sets, and Splay Trees are built to optimize performance in computations where speed and scalability matter most. In this article, we will explore their operations, visual representations, and practical implementation examples.

Why Advanced Data Structures?

In modern computing, operations like real-time range queries, dynamic graph processing, and efficient memory management demand more than simple data structures. Advanced structures allow:

• Efficient query resolution in logarithmic or near-constant time.
• Optimized space management for large-scale storage systems.
• Dynamic adaptability for real-world use cases like databases, network routing, and compilers.

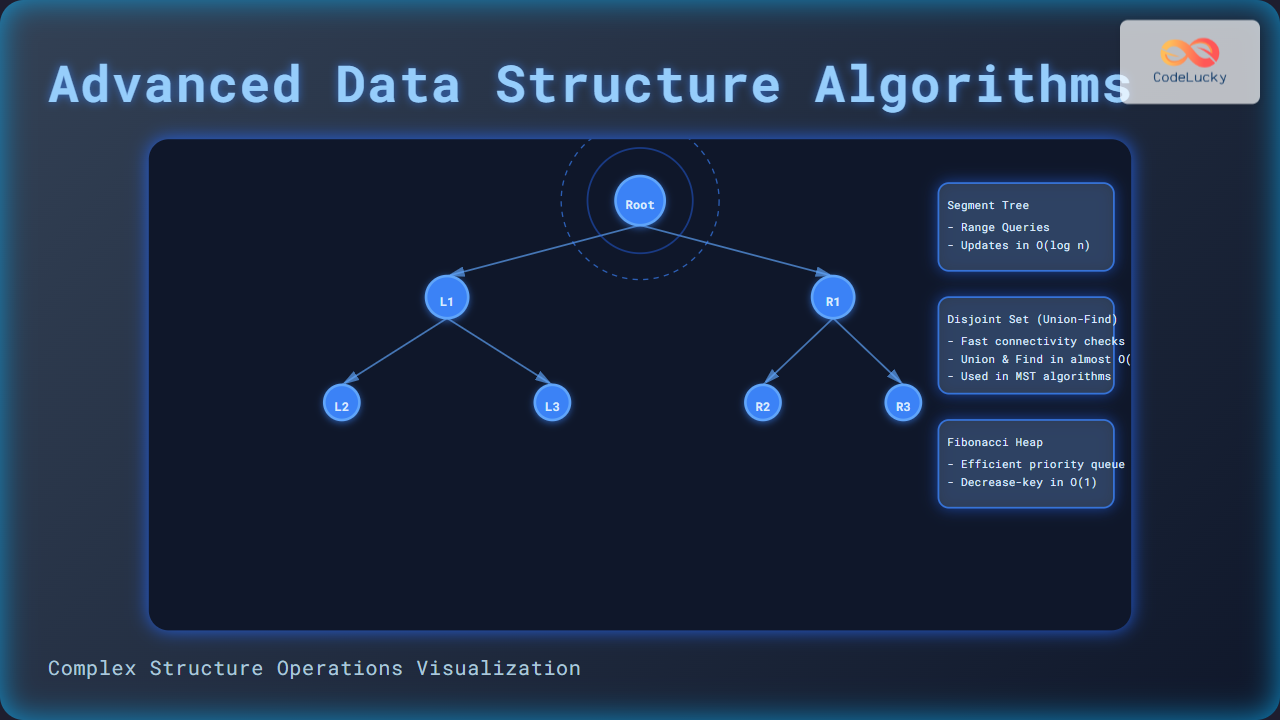
Segment Trees: Range Query Optimization

A Segment Tree is a binary tree used to answer range queries efficiently, such as sum, minimum, or maximum over a segment of an array. It allows both updates and queries in O(log n) time.

Example: Find the sum of elements between index 2 and 6 in an array using a segment tree.

class SegmentTree:
    def __init__(self, arr):
        self.n = len(arr)
        self.tree = [0] * (2 * self.n)
        for i in range(self.n):
            self.tree[self.n + i] = arr[i]
        for i in range(self.n - 1, 0, -1):
            self.tree[i] = self.tree[2 * i] + self.tree[2 * i + 1]

    def query(self, l, r):
        res = 0
        l += self.n
        r += self.n + 1
        while l < r:
            if l % 2:
                res += self.tree[l]
                l += 1
            if r % 2:
                r -= 1
                res += self.tree[r]
            l //= 2
            r //= 2
        return res

Output: For array [1, 2, 3, 4, 5, 6, 7], querying (2,6) returns 25.

Fibonacci Heaps: Priority Queue Efficiency

A Fibonacci Heap supports insert, merge, and decrease-key operations with better amortized complexity than a binary heap. It is especially impactful in graph algorithms like Dijkstra’s shortest path.

Key Properties:

• Insert in O(1) amortized.
• Decrease key in O(1) amortized.
• Extract-min in O(log n) amortized.

Disjoint Set (Union-Find): Fast Connectivity Checks

The Disjoint Set Union (DSU) or Union-Find data structure efficiently checks whether elements are in the same set and unites two sets. It is frequently used in Kruskal’s Minimum Spanning Tree algorithm.

class DSU:
    def __init__(self, n):
        self.parent = list(range(n))
        self.rank = [0] * n

    def find(self, x):
        if self.parent[x] != x:
            self.parent[x] = self.find(self.parent[x])
        return self.parent[x]

    def union(self, x, y):
        xr, yr = self.find(x), self.find(y)
        if xr == yr:
            return False
        if self.rank[xr] < self.rank[yr]:
            self.parent[xr] = yr
        elif self.rank[xr] > self.rank[yr]:
            self.parent[yr] = xr
        else:
            self.parent[yr] = xr
            self.rank[xr] += 1
        return True

Example: Efficient connectivity check in dynamic graphs → O(α(n)), where α is the inverse Ackermann function.

B-Trees: Balanced Disk-Based Storage

B-Trees are self-balancing search trees where every node can have multiple children. They are used in databases and filesystems because they minimize disk read operations.

Advantages:

• Balanced search time O(log n).
• Efficient for large blocks of data.
• Ideal for databases and indexing systems.

Splay Trees: Adaptive Self-Adjusting Operations

Splay Trees are self-adjusting binary search trees. After every access, they apply rotations to move the accessed element closer to the root, optimizing frequently accessed elements.

Use Case: Ideal for adaptive systems where repeated access of elements benefits from faster retrieval.

Conclusion

Advanced data structure algorithms form the backbone of efficient computing systems. From range queries and dynamic connectivity to database indexing and priority optimization, these structures optimize performance-critical applications. Mastery of these concepts allows developers and computer scientists to handle large-scale problems with efficiency and elegance.